第 6 章 数据分析
第6.1节基于小麦产量数据建立空间线性混合效应模型,以 R 软件和相关 R 包为工具,介绍空间统计建模分析的过程,特别是诊断和添加空间随机效应的分析方法和模型参数初值的确定方式。这个分析方法和初值的确定方式具有普适性,对于更复杂的空间广义线性混合效应模型也是适用的。第6.2节建立响应变量服从泊松分布的空间广义线性混合效应模型分析一个真实数据集 rongelap。rongelap 数据集目前由 Christensen 维护在 R 包 geoRglm 里,曾被 Diggle 等 (1998年) (Diggle, Tawn, and Moyeed 1998) 、Christensen (2004年) (Christensen 2004) 和 Ribeiro 和 Bonat (2016年) (Bonat and Ribeiro Jr. 2016) 分析过,第 6.2 节首先分别基于第4章第4.4.2小节介绍的蒙特卡罗极大似然算法和第4.4.1小节介绍的拉普拉斯近似算法估计泊松型空间广义线性混合效应模型的参数,与他们不同的是,这里进一步根据不同的初始值观察迭代陷入局部极值点或者由于似然曲面太平坦致使迭代终止的情况,因此提出结合第4章第4.2节介绍的剖面似然函数的想法,借助剖面似然函数轮廓来确定更加合适的初值。
6.1 小麦产量的空间分布
Stroup 和 Baenziger (1994年) (Stroup and Baenziger 1994) 采用完全随机的区组设计研究小麦产量与品种等因素的关系,在 4 块肥力不同的地里都随机种植了 56 种不同的小麦, 实验记录了小麦产量、品种、位置以及土地肥力等数据, Pinheiro 和 Bates (2000年) (Pinheiro and Bates 2000) 将该数据集命名为 Wheat2 ,整理后放在 nlme 包里。 利用该真实的农业生产数据构建带空间效应的线性混合效应模型,与上述文献不同的是详述选初值、诊断和添加空间效应的过程。
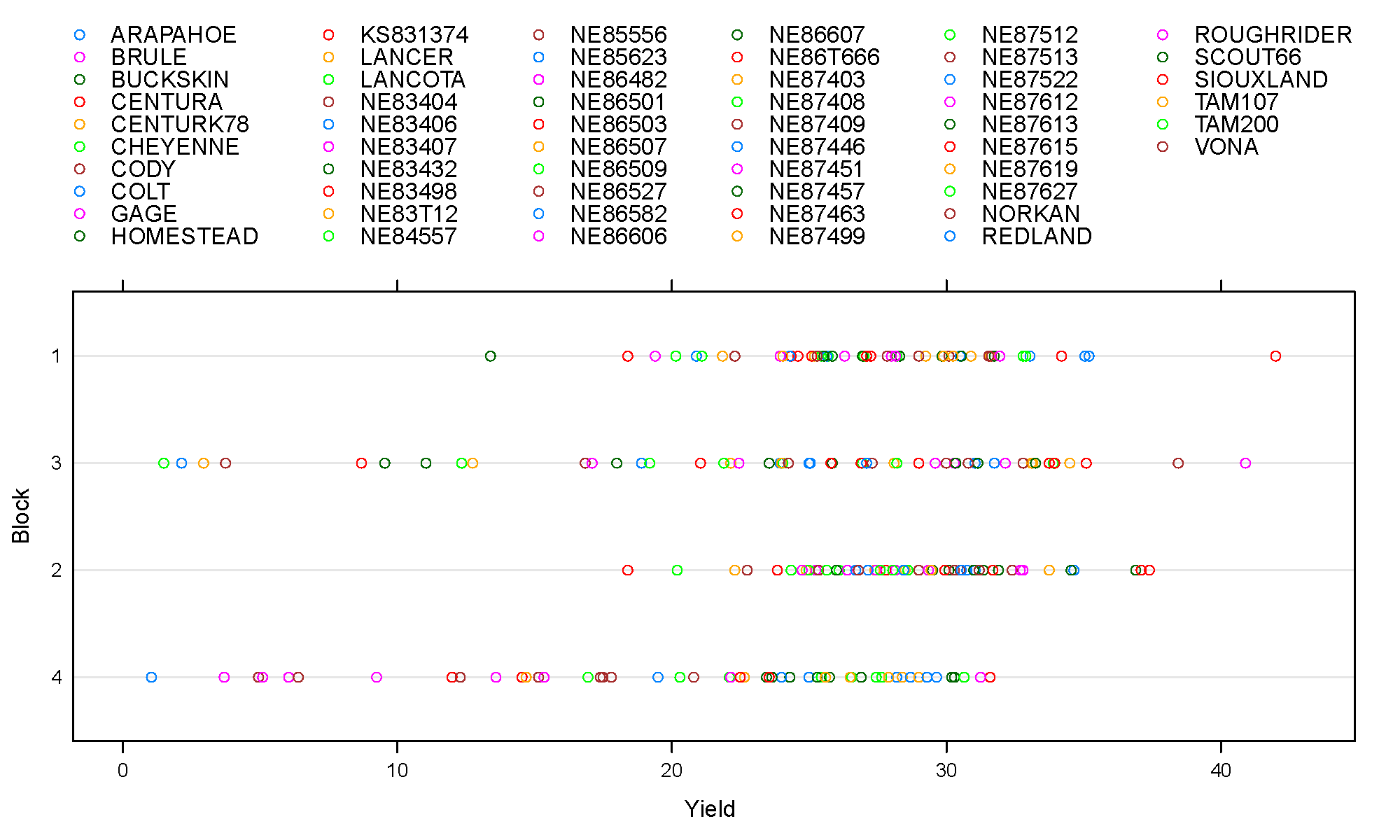
图 6.1: 小麦产量与土壤肥力的关系,图中纵轴表示试验田的4种类型,且土壤肥力强弱顺序是 1 > 2 > 3 > 4,横轴表示小麦产量,每块试验田都种植了 56 种小麦,图中分别以不同的颜色标识,图上方是小麦类型的编号
图 6.1 按土壤肥力不同分块展示每种小麦的产量,图中暗示数据中有明显的 block 效应,即不同实验田对结果产生显著影响,而且不同实验田之间,小麦产量呈现异方差性,为了更好地表达这些效应,可以基于经纬度坐标信息添加与空间相关的结构 (spatial correlation structures)。基于上述对图6.1 的探索,先建立一般的线性模型,以量化上述描述性分析结果,模型结构如下
\[\begin{equation}
y_{ij} = \tau_i + \epsilon_{ij}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0},\sigma^2 \boldsymbol{\Lambda}) \tag{6.1}
\end{equation}\]
其中,\(y_{ij}\) 表示第 \(i\) 种小麦在第 \(j\) 块试验田里的产量,\(i = 1,\ldots,56\),\(j = 1,\ldots,4\)。 \(\tau_i\) 表示第 \(i\) 种小麦的平均产量,\(\epsilon_{ij}\) 是随机误差,假定服从均值为 0,协差阵为 \(\sigma^2 \boldsymbol{\Lambda}\) 的多元正态分布。进一步,继续探索线性模型(6.1)中的协方差 \(\boldsymbol{\Lambda}\) 的结构,不妨先假定模型 (6.1) 的随机误差是独立且方差齐性的,即 \(\boldsymbol{\Lambda} = \boldsymbol{I}\) 。接着,需要确认方差齐性的假设是否合适,拟合残差散点图是一个有用又方便的判断工具。特别地,对于空间效应的探索,采用样本变差图探索数据中存在的空间相关性,可调用 nlme 包中的 Variogram 函数获得 gls 函数拟合方差齐性的线性模型的变差图6.2,横坐标是小麦之间的欧氏距离,纵坐标是样本变差,图中的平滑线根据局部多项式拟合的方法添加,用以估计样本变差的大致趋势。
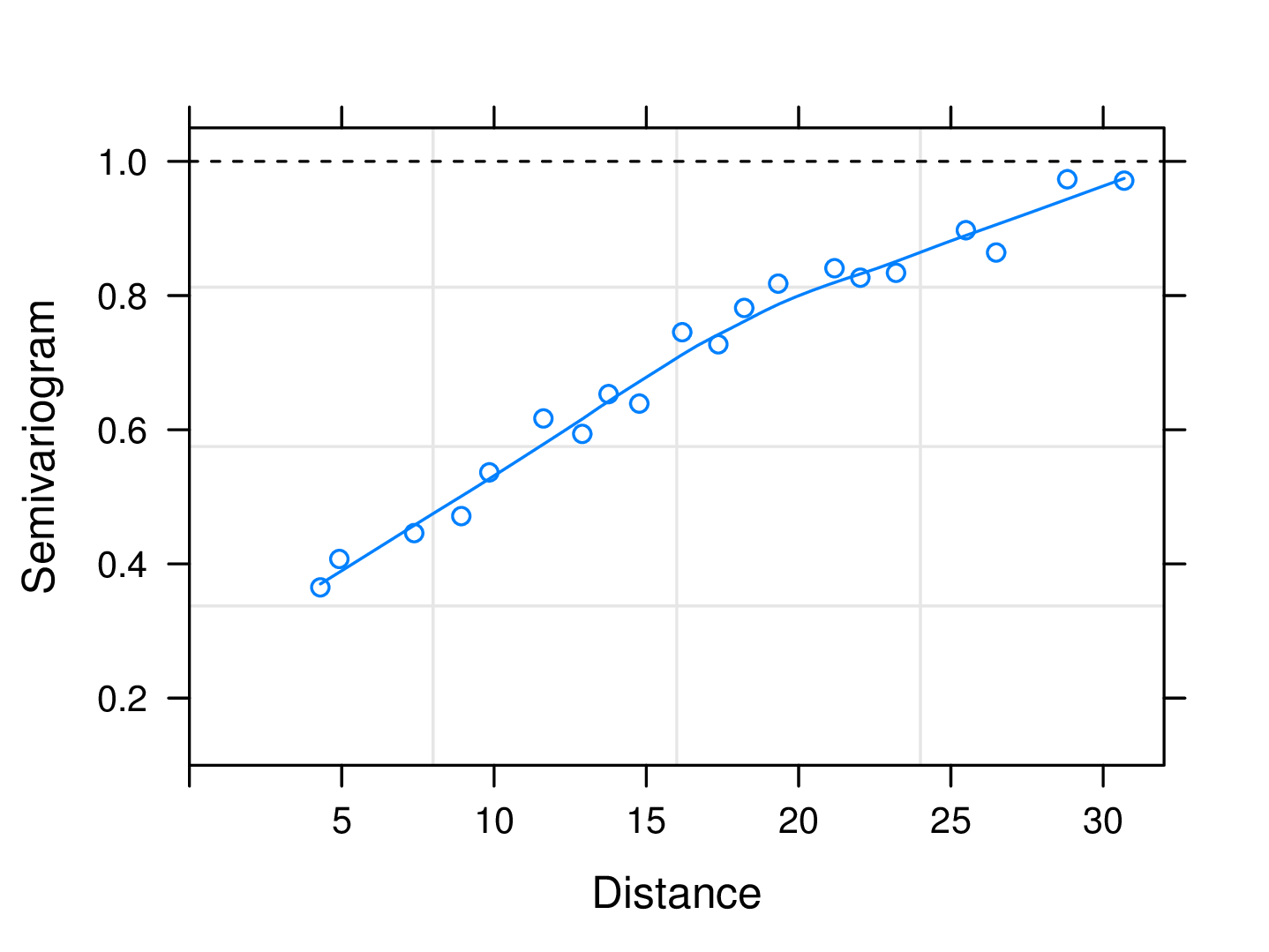
图 6.2: 样本变差散点图
图 6.2 显示样本变差随空间距离有明显的增长趋势,可见空间随机效应明显,根据第3章第3.4.2小节,可以有理由地估计块金效应\(\tau^2\)大约是 0.2,参数 \(\phi\) 可由样本变差为 1 对应的空间距离来初步估计,图6.2显示该值大约是 31。 图中的平滑曲线是 局部多项式回归拟合的结果,也可以用局部加权回归拟合的平滑法来确定初值 (谢益辉 2008)。上述图示分析,首先采用球性自相关函数拟合这组数据中的空间结构。考虑空间效应后,采用 gls 函数提供的限制极大似然法 (Restricted Maximum Likelihood Estimation, 简称 REML) 拟合模型(6.1),与第2章第2.3节介绍的极大似然估计相比,它对方差分量的估计偏差更小一些(Peter J. Diggle and Ribeiro Jr., n.d.),适合估计线性混合效应模型的参数,gls 还支持不同类型的空间自相关函数,因此继续探索球型和二次有理型自相关函数3对模型拟合结果的影响。以小麦数据为例估计空间线性混合效应模型的参数,见表6.1,表中\(\phi_0,\tau^2_{0},\sigma^2_{0}\)和\(\hat{\phi},\hat{\tau}^2,\hat{\sigma}^2\)分别是模型(6.1)参数\(\phi,\tau^2,\sigma^2\)的初值和估计值。
| 自相关函数 | \(\hat{\phi}(\phi_0)\) | \(\hat{\tau}^2(\tau^2_{0})\) | \(\hat{\sigma}^2(\sigma^2_{0})\) | log-REML | |
|---|---|---|---|---|---|
| I | 球型 | \(1.515\times 10^{5}(31)\) | \(5.471\times 10^{-5}(0.2)\) | 466.785 | -533.418 |
| II | 二次有理型 | \(13.461(13)\) | \(0.193(0.2)\) | 8.847 | -532.639 |
| III | 球型 | \(27.457(28)\) | \(0.209(0.2)\) | 7.410 | -533.931 |
表6.1中二次有理型自相关函数 \(\rho(u) = (u/\phi)^2/[1 + (u/\phi)^2]\),则半变差函数 \(V(u) = 1-\rho(u) = [\tau + (u/\phi)^2]/[1 + (u/\phi)^2]\)。当距离 \(u = \phi\) 时,变差等于 \((1+\tau)/2\),由图6.2可知 \(\tau = 0.2\), 样本变差就等于 0.6 对应的距离,大约是 13,所以 \(\phi=13\)。

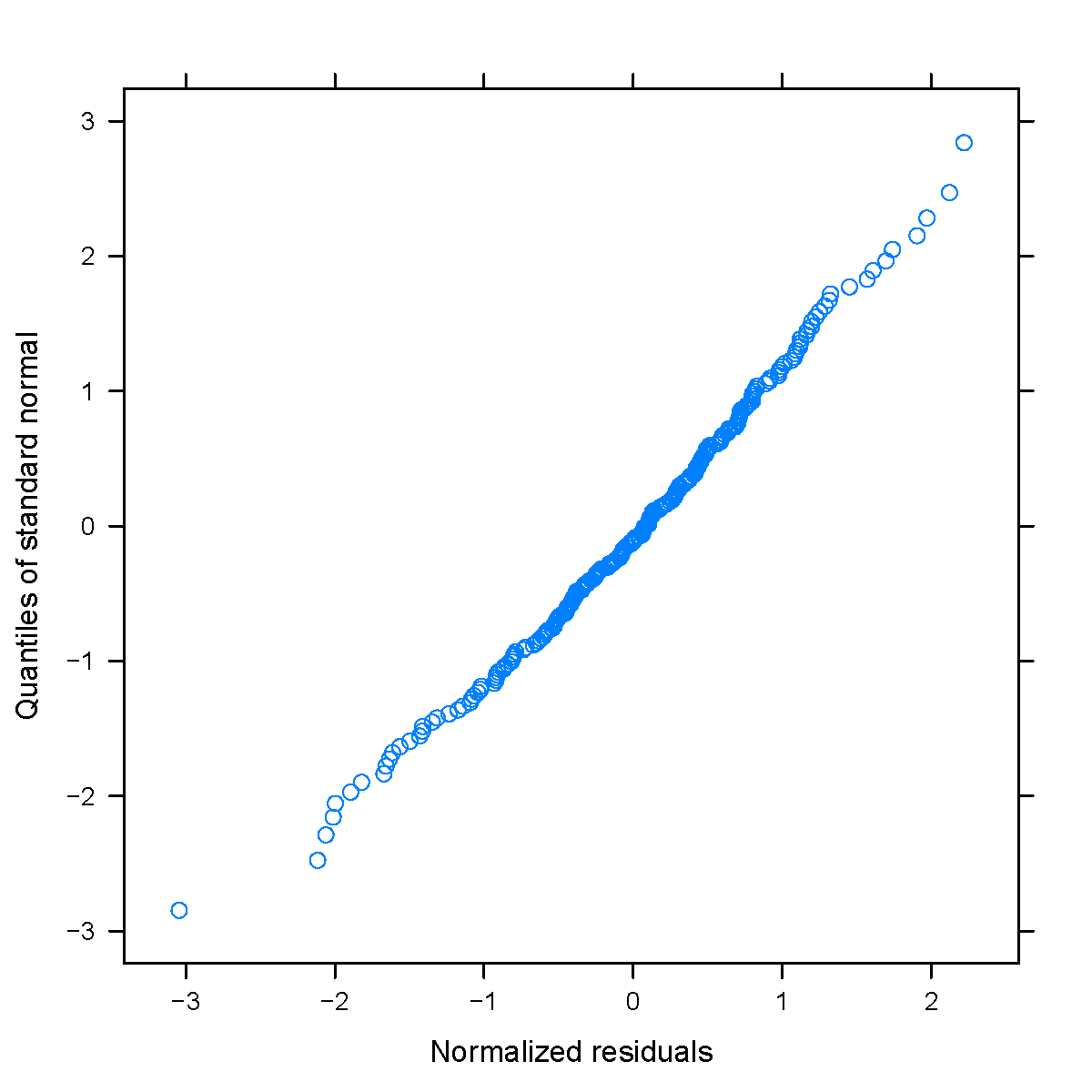
图 6.3: 模型拟合后的残差诊断
值得注意的是,用限制极大似然法估计模型 (6.1) 的参数时,对初始值很敏感,通过几番试错调整初值获得如表 6.1 所示结果。根据表6.1, 可以得出两个结论,其一选择合适的自相关函数可以取得更好的拟合效果,其二限制极大似然算法对初值很敏感,不断试错以选择合适的初值很重要。最后,再来观察使用空间线性混合效应模型拟合小麦数据后的标准化残差图,如图 6.3 所示,残差中空间效应已经提取得很充分了。6.3(a) 横轴表示模型的拟合值,纵轴是标准化后的残差值, 6.3(b)横轴表示标准化后的残差值,纵轴表示标准正态分布的分位数。
6.2 核污染浓度的空间分布
朗格拉普岛位于南太平洋上,是马绍尔群岛的一部分,二战后,美国在该岛上进行了多次核武器测试,核爆炸后产生的放射性尘埃笼罩了全岛,目前该岛仍然不适合人类居住,只有经批准的科学研究人员才能登岛。基于马绍尔群岛国家的放射性调查数据,Diggle 等 (1998年) (Diggle, Tawn, and Moyeed 1998) 使用 蒙特卡罗极大似然算法估计空间广义线性混合效应模型 (6.2) 的各个参数,Christensen (2004年) (Christensen 2004) 发现该核污染数据集中存在不能被泊松分布解释的残差,因此添加了非空间的随机效应 \(Z_i\),建立模型 (6.3),在地质统计领域内,\(Z_i\) 还有个专有名词叫块金效应。 \[\begin{align} \log\{\lambda(x_{i})\}& = \beta + S(x_{i}) \tag{6.2}\\ \log\{\lambda(x_{i})\}& = \beta + S(x_{i}) + Z_{i} \tag{6.3} \end{align}\] 放射性调查获得的 rongelap 数据集包含几个观测变量,分别是放射粒子数、相应时间间隔和157个空间坐标。为了增加直观性,绘制图6.4 展示收集放射性数据的观测站点的空间分布,图中加号 + 标注采样的位置,水平方向表示横坐标,垂直方向表示纵坐标。
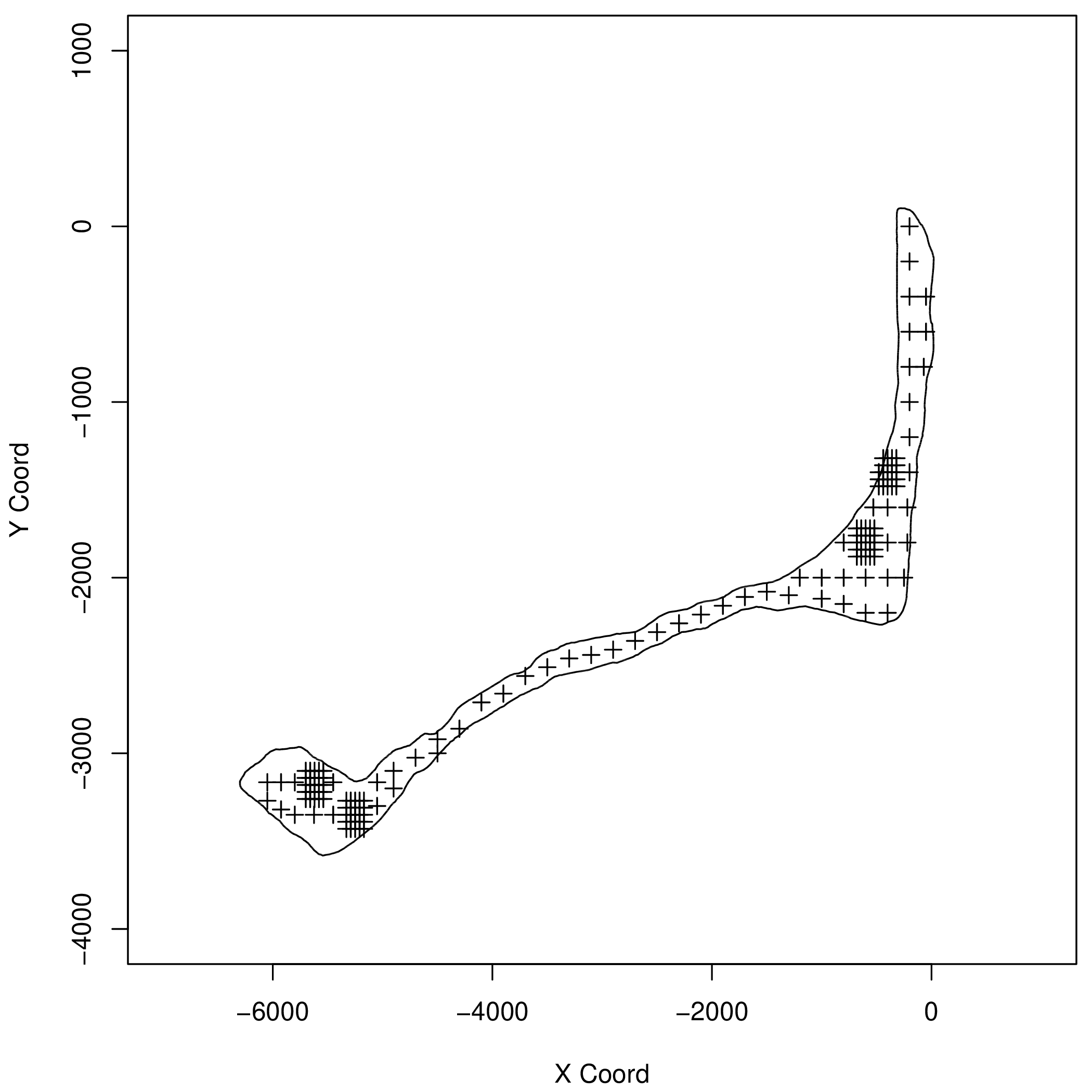
图 6.4: 朗格拉普岛上157个观察站点的空间位置
根据 \({}^{137}\mathrm{Cs}\) 放出的伽马射线在 \(N=157\) 站点不同时间间隔的放射量, 建立泊松广义线性混合效应模型 (6.3)。模型(6.3)中,\(\beta\) 是截距, 放射粒子数作为响应变量服从强度为 \(\lambda(x_i)\) 的泊松分布,即 \(Y_{i} \sim \mathrm{Poisson}( \lambda(x_i) )\),平稳空间高斯过程 \(S(x),x \in \mathbb{R}^2\)的自协方差函数为 \(\mathsf{Cov}( S(x_i), S(x_j) ) = \sigma^2 \exp( -\|x_i -x_j\|_{2} / \phi )\),且 \(Z_i\) 之间相互独立同正态分布 \(\mathcal{N}(0,\tau^2)\),这里 \(i = 1,\ldots, 157\)。
蒙特卡罗极大似然算法迭代的初值 \(\beta_{0} = 6.2,\sigma^2_{0} = 2.40,\phi_{0} = 340,\tau^2_{rel} = 2.074\),模拟次数为 30000 次,前 10000 次迭代视为预处理阶段,其后每隔 20 次迭代采一个样本点,即存储模型各参数的迭代值,每个参数获得1000次迭代值。蒙特卡罗模拟平稳空间高斯过程 \(S(x)\) 关于响应变量\(Y\)的条件分布时,使用了第4章第4.4.3节介绍的 Langevin-Hastings 算法 (Papaspiliopoulos 2003)。此处,157 个站点意味着有 157 个条件分布需要模拟,共产生 157个迭代链,每条链需保持平稳才可用于模型参数的估计。因此,需要先检验每条链的平稳性,可以采用自相关图和时序图来检验,篇幅所限,取部分站点展示,图6.5 是四个站点处的后验分布的模拟过程图,图 6.6 是9个站点处的模拟点列的自相关系数图。从图 6.5 可以看出迭代序列符合平稳性的特征,从图 6.6 可以看出迭代序列满足马尔科夫性,没有明显的延迟相关性。经观察 157 个站点处的\(S_i\)的迭代点列没有出现不平稳的现象。
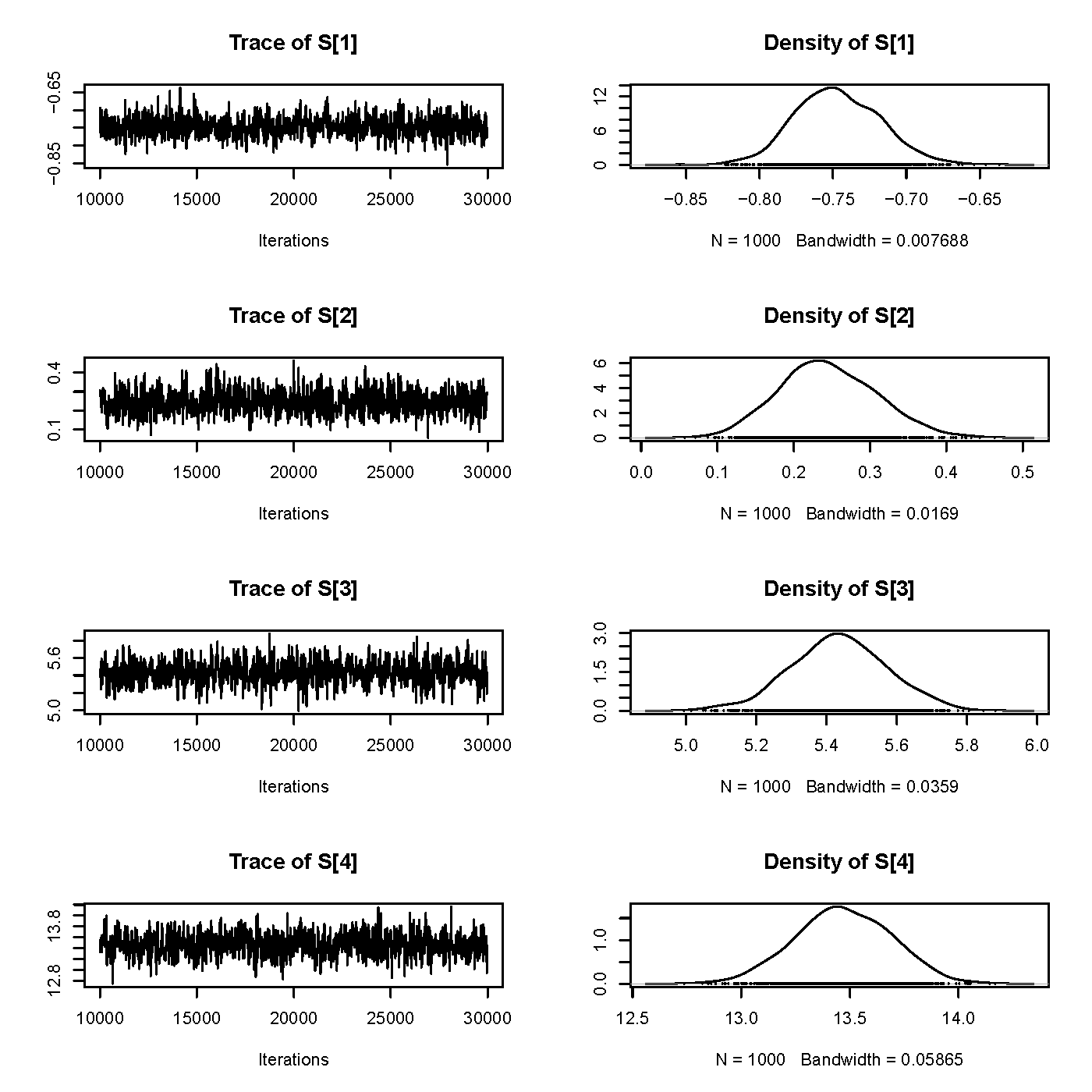
图 6.5: Langevin-Hastings 算法模拟条件分布 \(S(x_{i})|Y_{i}, i = 1,\ldots,4\),第一列是迭代序列轨迹图,第二列是对应的后验密度分布
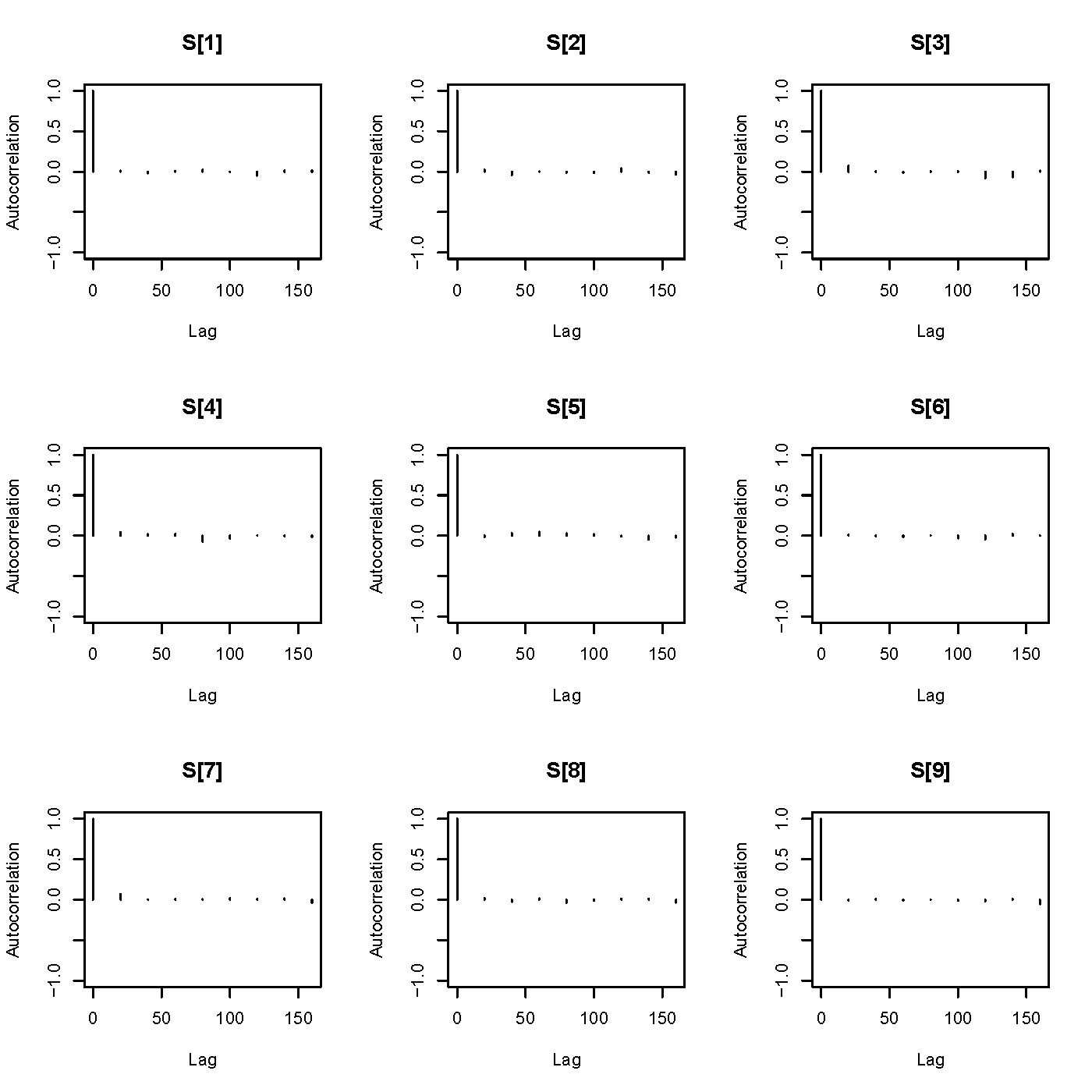
图 6.6: 条件分布 \(S(x_{i})|Y_{i}, i = 1, \ldots, 4\) 的采样序列的自相关图
表 6.2 中括号内表示相应模型参数的初值,以第4行为例,模型(6.3)中块金效应的估计值应为 \(\hat{\tau}^2 = \hat{\sigma}^{2} \times \hat{\tau}^2_{rel} = 4.929\),第 2 行是基于第4章第4.4.1小节介绍的拉普拉斯近似极大似然算法(简称LAML)获得的结果,第 3 行基于蒙特卡罗极大似然算法(简称MCML)获得的结果,其初值选择和 LAML 算法一致,第 4 行先根据剖面似然轮廓图6.7确定初值,然后根据MCML算法获得参数估计值。第6列是最终参数估计值处的对数似然函数值。
| 算法 | \(\hat{\beta}(\beta_{0})\) | \(\hat{\sigma}^{2}(\sigma^2_0)\) | \(\hat{\phi}(\phi_0)\) | \(\hat{\tau}^2_{rel}(\tau^2_{rel_0})\) | \(\log L_{m}\) |
|---|---|---|---|---|---|
| LAML | 1.821(2.014) | 0.264(0.231) | 151.795(50) | 0.133(0.1) | \(-1317.195\) |
| MCML | 1.821(2.014) | 0.265(0.231) | 151.859(50) | 0.132(0.1) | \(-8.8903\) |
| MCML | 6.190(6.200) | 2.401(2.400) | 338.126(340) | 2.053(2.074) | \(-5.8458\) |
由于两个算法所采用的方法不同,前者采用拉普拉斯近似似然函数中的高维积分,并且扔掉了似然函数中的正则常数,后者采用蒙特卡罗模拟计算高维积分,所以对数似然函数值差别很大,两种算法之间不能以这个比较算法优劣。
表6.2第3和第4行的设置是同种算法不同初始值的比较,可以比较最终的似然函数值,后者初值选得好,对数似然函数值更大,同时结合图 6.7 有理由怀疑前一组初值使得最终的迭代陷入一个局部极值点或者由于似然曲面太平坦致使迭代停止。 图6.7是泊松型空间广义线性混合效应模型 (6.3) 关于参数 \(\phi\) 和相对块金效应 \(\tau^2_{rel} = \tau^2 / \sigma^2\) 的剖面似然函数轮廓图,平稳空间高斯过程 \(S(x)\) 的自协方差函数选用指数型 \(\mathsf{Cov}( S(x_i), S(x_j) ) = \sigma^2 \exp( -\|x_i -x_j\|_{2} / \phi )\),剖面似然函数值由 geoRglm 包提供的 proflik.glsm 函数计算。
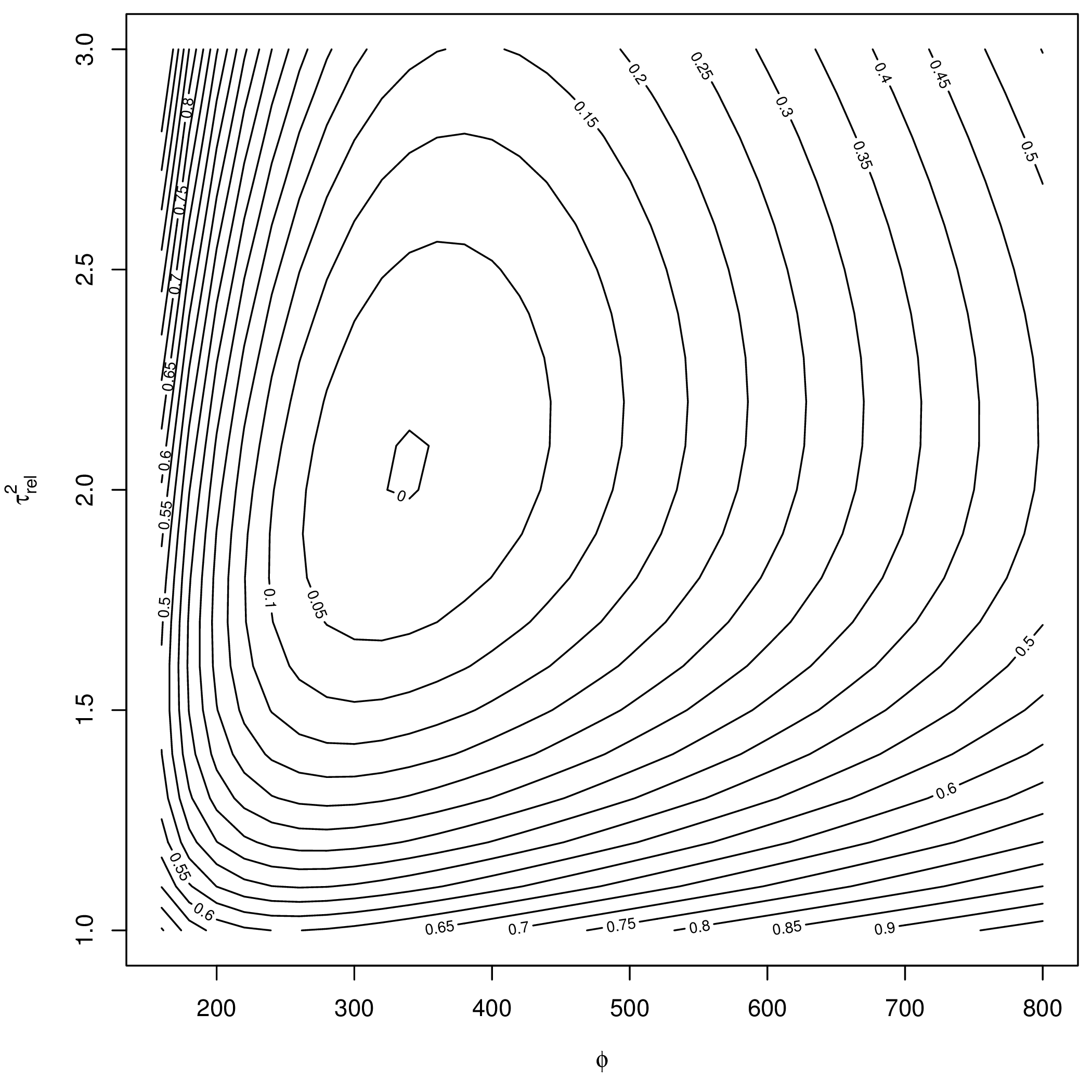
图 6.7: 模型 (6.3) 关于参数 \(\phi\) 和 \(\tau^2_{rel} = \tau^2 / \sigma^2\) 的剖面似然函数轮廓图
由表 6.2 可知,正如第 5 章第 5.3 节对蒙特卡罗极大似然算法所指出的那样,必须提供足够接近真值的初值,才能获得好的参数估计。由图 6.7 不难看出,关于 \(\phi\) 和相对块金效应 \(\tau^2_{rel}\) 的剖面似然函数曲面类似一个极其狭长的、坡度又平缓的山谷,基于似然的算法对这种类型的问题还没有好的解决办法,目前取多个不同参数初值进行迭代,用迭代值画出剖面似然函数曲面,然后通过观察获得最佳初值。从实践的过程来看,参数初值的组数不宜太多,过多可能会用掉不少计算资源,因为如第4章第4.2节剖面似然估计所指出的迭代过程,剖面似然函数值的计算涉及空间随机效应的协方差阵的求逆,当空间采样点数目较多时,协方差阵阶数会随着变大,计算会变困难。
6.3 本章小结
从小麦数据和核污染数据的似然分析中,可以清晰地看到模型参数初值对求似然函数极值点的重要性。借助变差图等可视化手段探索模型结构,确定初值是很有意义的,在小麦数据的分析过程中,并不是一步到位地给出空间线性混合效应模型,而是给出了模型从简单到复杂的建模过程,这对于实际应用有指导意义。对核残留数据集,建立了泊松型空间广义线性混合效应模型,其似然分析则借助了剖面似然估计的思想,将一个含有多个参数的未知似然函数降至只有两维的剖面似然函数曲面,再对似然曲面的分析获得最佳初始值的位置,最后根据蒙特卡罗最大似然算法获得了近似全局最优的参数估计值。
参考文献
Diggle, Peter J., J. A. Tawn, and R. A. Moyeed. 1998. “Model-Based Geostatistics.” Journal of the Royal Statistical Society, Series C 47 (3): 299–350.
Christensen, Ole F. 2004. “Monte Carlo Maximum Likelihood in Model-Based Geostatistics.” Journal of Computational and Graphical Statistics 13 (3): 702–18.
Bonat, Wagner Hugo, and Paulo J. Ribeiro Jr. 2016. “Practical Likelihood Analysis for Spatial Generalized Linear Mixed Models.” Environmetrics 27 (2): 83–89.
Stroup, Walter W., and P. Stephen Baenziger. 1994. “Removing Spatial Variation from Yield Trials: A Comparison of Methods.” Crop Science 34 (1): 63–66.
Pinheiro, Jos C., and Douglas M. Bates. 2000. Mixed-Effects Models in S and S-PLUS. New York, NY: Springer-Verlag.
谢益辉. 2008. “用局部加权回归散点平滑法观察二维变量之间的关系.” https://cosx.org/2008/11/lowess-to-explore-bivariate-correlation-by-yihui.
Diggle, Peter J., and Paulo J. Ribeiro Jr. n.d. Model-Based Geostatistics. New York, NY: Springer-Verlag.
Papaspiliopoulos, Omiros. 2003. “Non-Centered Parameterisations for Data Augmentation and Hierarchical Models with Applications to Inference for Lèvy-Based Stochastic Volatility Models.” PhD thesis, Lancaster: Lancaster University.
详见 R 包 nlme 内函数 corRatio 帮助文档。↩