第 1 章 历史
“这易如反掌，”他说，“我看到你左脚穿的那只鞋的内侧，也就是炉火刚好照到的地方，皮面上有六道几乎平行的划痕。显然，这些划痕是有人为了去掉沾在鞋跟上的泥疙瘩，极其粗心大意地顺着鞋跟刮泥而造成的。因此，现在你就明白了我得出的这两个推断：其一，你曾经在恶劣的天气外出过；其二，你穿的皮靴上面的特别难看的划痕是伦敦的女佣所为。至于你开业行医，这么说吧，如果一位先生走进我的房间，身上带有碘的气味，右手食指上有硝酸银腐蚀的黑斑，高顶黑色大礼帽的右侧鼓起一块，那里面藏着听诊器，而我不断言他是医务界的一位活跃分子，那我不是太迟钝了吗？
— 柯南·道尔《波希米亚丑闻》
统计图形的意义在于引导我们观察到统计数据中的信息。用著名统计学家 John Tukey 的话来讲，就是“图形的最大价值就是使我们注意到我们从来没有料到过的信息”（The greatest value of a picture is when it forces us to notice what we never expected to see）。从这个意义上讲，统计图形的重要性自然不言而喻。
在统计图形历史上，能够达到“揭示人们不曾料到的信息”这种高度的图形并不多，那么这里我们首先欣赏几幅前人创造出的名垂青史的统计图形。
1.1 饼图和线图的起源
饼图和线图都是当今社会中常用的统计图形，它们是由有着“统计图形奠基人”之称的苏格兰工程师兼政治经济学家 William Playfair 发明的。在 “The Commercial and Political Atlas” (Playfair 1786) 一书中，他用线图展示了英格兰自 1700 年至 1780 年间的进出口数据（如图 1.1），从图中可以很清楚看出对英格兰有利和不利（即顺差、逆差）的年份；而在 “The Statistical Breviary” (Playfair 1801) 一书中，他第一次使用了饼图来展示一些欧洲国家的领土比例，图 1.2 即为史上第一例饼图。从下方的饼图中我们可以清楚看出当时的土耳其帝国分别在亚洲、欧洲和非洲的领土面积比例。这两幅图在今天看来似乎没有什么惊世骇俗之处，但在当时统计图形种类极为稀少的年代，能以这种方式清晰展示数据结构，也实属难能可贵。除了这两种图形之外，他还发明了条形图和圆环图。
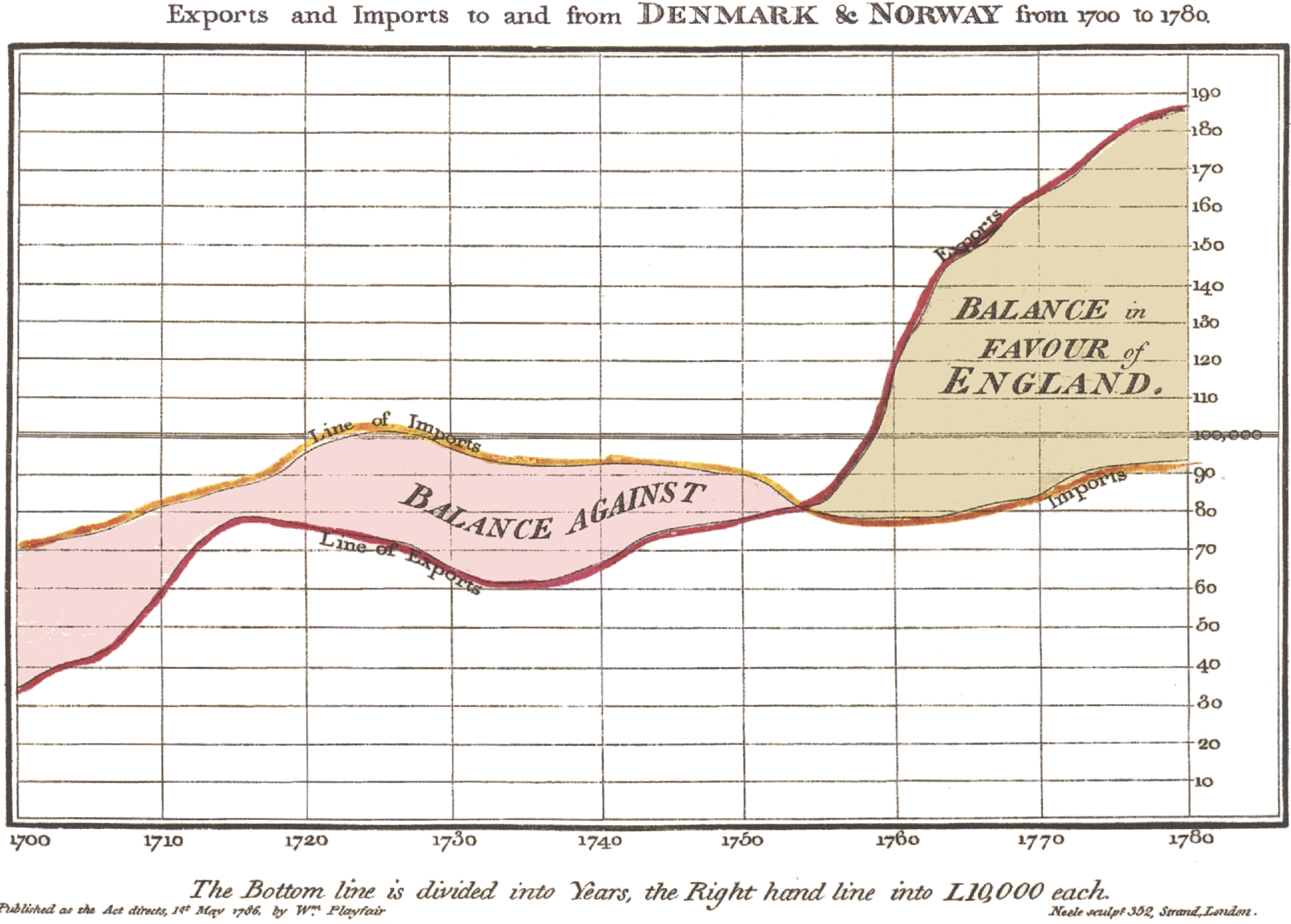
图 1.1: Playfair (1786) 绘制的线图。 这幅图主要展示了 1700 年至 1780 年间英格兰的进出口时序数据，左边表明了对外贸易对英格兰不利，而随着时间发展，大约 1752 年后，对外贸易逐渐变得有利。图片来源： https://en.wikipedia.org/wiki/William_Playfair
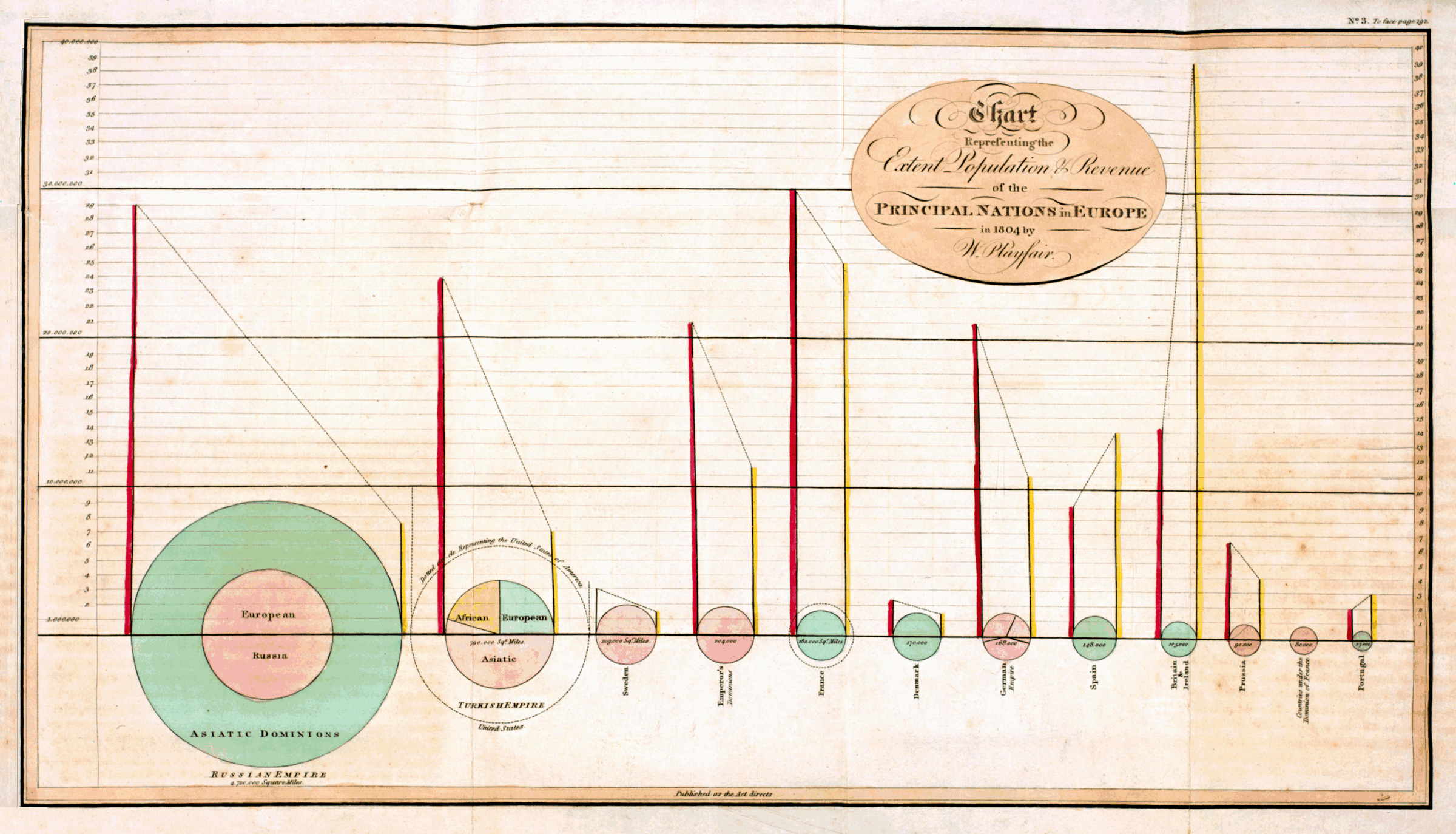
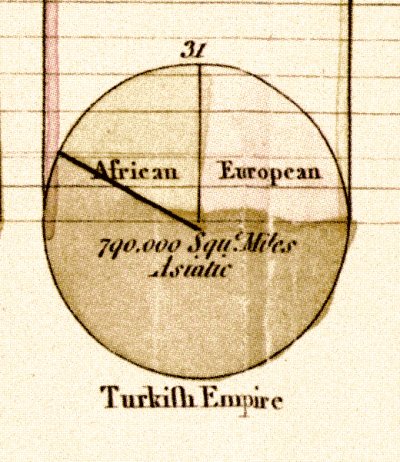
图 1.2: Playfair (1801) 绘制的饼图。这是历史上最早出现的饼图，描述了法国大革命前后一些欧洲国家的统计数据。上方的大图展示了各个国家的领土面积（和圆圈成比例）以及人口（左垂线）、税收（右垂线）、国土在各大洲分布比例等数据，两条垂线连线的斜率可表示税负的轻重（这一点颇有争议，因为斜率与圆的半径有关）。下方的饼图展示了土耳其帝国在三大洲的国土面积分布。图片来源：https://en.wikipedia.org/wiki/William_Playfair，https://www.math.usu.edu/~symanzik/papers/2009_cost/editorial.html
1.2 霍乱传染之谜
袭击欧洲大城市最严重的天灾要数 19 世纪的霍乱。由于垃圾没有得到及时清理，清洁水源的缺少，以及下水管道系统的不足，伦敦成为无药可医的流行病滋生的最佳地点。公众一致认为霍乱是由空气传播的，如果呼吸到了“瘴气”或者接触到霍乱患者，就会染上这种病。医生兼自学成才的科学家 John Snow 对这个观点颇为怀疑，他决心通过彻底调查这种致命疾病的根源来证实他的怀疑。
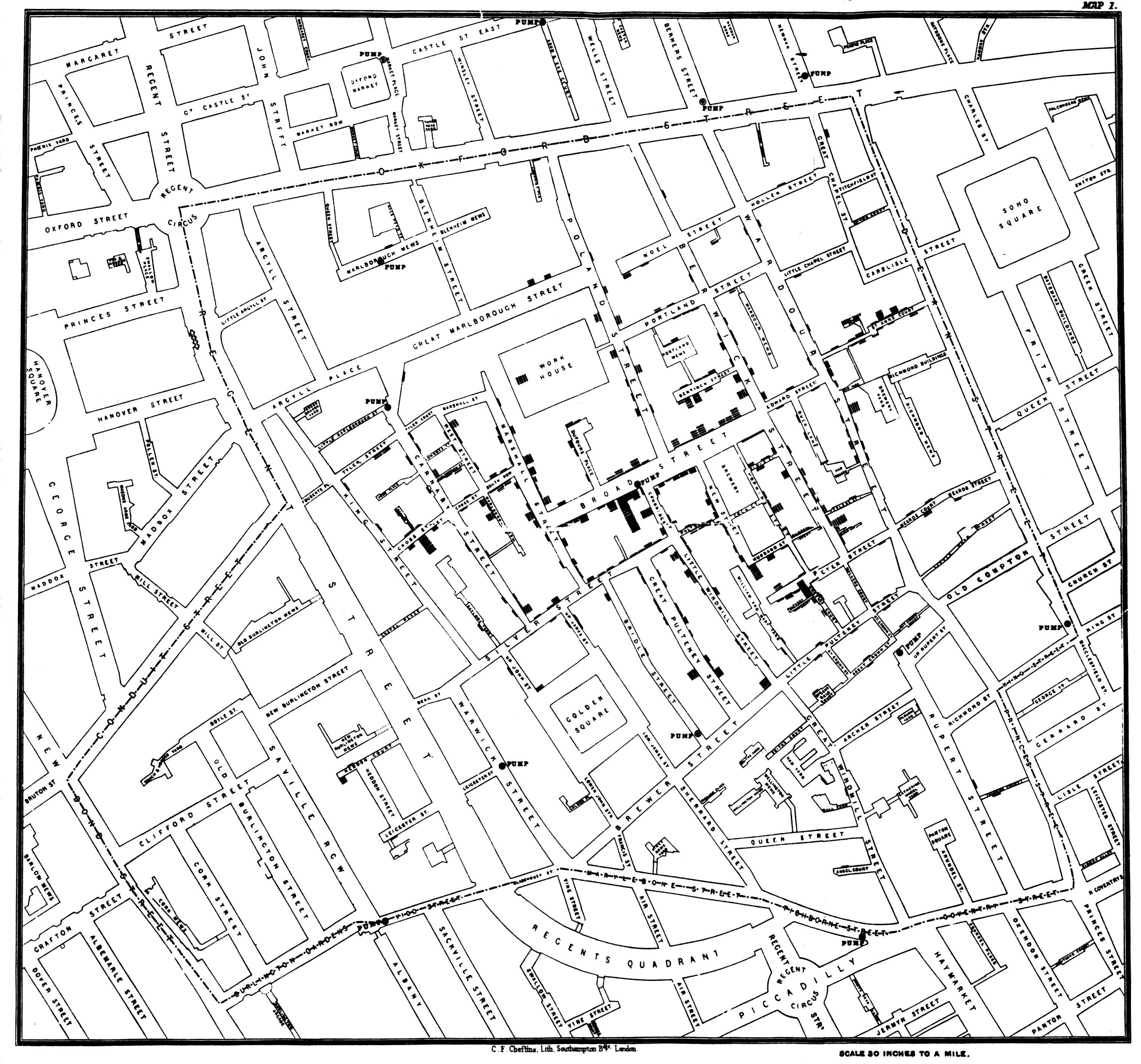
通过和当地居民交谈，他确定了霍乱爆发的源头是位于 Broad 大街的公共水泵。他对这种疾病类型的研究看起来很可信，因此他成功说服了当地政府废弃那个水泵。他所利用的主要证据就是图 1.3：死亡发生的地点有明显的地理规律，在这种规律的指引和相关调查证据的支持下，他最终确定了霍乱的源头。后来证实离这口井仅三英尺远的地方有一处污水坑，坑内释放出来的细菌正是霍乱发生的罪魁祸首。
图 1.3: 1854 年英国 Broad 大街大规模爆发霍乱，当时了解微生物理论的人很少，人们不清楚霍乱传播途径，而“瘴气传播理论”是当时的主导理论；John Snow 对这种理论表示了怀疑，于 1849 年发表了关于霍乱传播理论的论文，本图即其主要依据。图中心东西方向的街道即为 Broad 大街，黑点表示死亡的地点，黑点叠加的高度相应表示了该处死亡人数。这幅图形揭示了一个重要现象，就是死亡发生地都在街道中部一处水源（水井）周围，市内其它水源周围极少发现死者。进一步调查他发现这些死者都饮用过这里的井水
1.3 提灯女士的玫瑰图
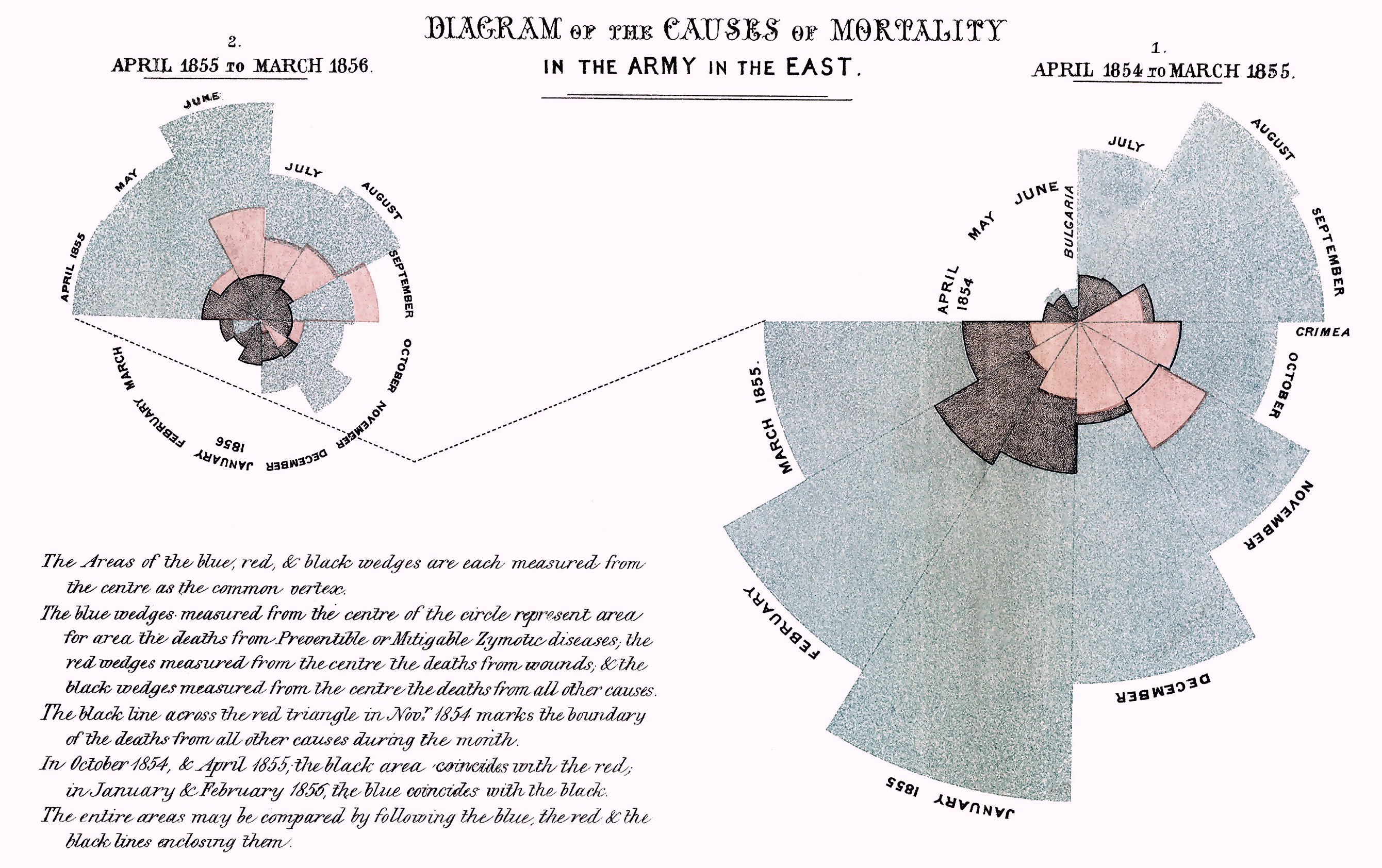
南丁格尔（Florence Nightingale）是我们耳熟能详的“提灯女士”，她不仅是现代护理的鼻祖及现代护理专业的创始人，而且是历史上使用极坐标面积图的先驱。这种图形外形如玫瑰，因此后来也称之为玫瑰图，其主要构思是用“花瓣”的面积表示统计数值的大小。图 1.4 反映了克里米亚战争（英国等与俄国争夺巴尔干半岛的战争）中英国军队自 1854 年 4 月至 1856 年 3 月的逐月死亡人数 (Nightingale 1858)；其中，右图为 1854 年 4 月至 1855 年 3 月的死亡人数，左图为 1855 年 4 月至 1856 年 3 月的死亡人数。玫瑰图不仅清楚展示了这两年军队死亡人数的变化，而且更重要的是，她将每个月中三种死亡情况也分别用不同颜色标记出来：蓝色表示死于可预防的疾病、红色表示死于战争伤害、黑色表示死于其它原因。这样我们可以清楚知道军队伤亡原因的结构，尤其是“绝大多数士兵死于可预防的疾病”（图中最高的花瓣）。凭借这一条重要信息，她让英国政府意识到，真正影响战争伤亡的并非战争本身，而是由于军队缺乏有效的医疗护理！
图 1.4: 南丁格尔的极坐标面积图：两幅图分别是 1854 年和 1855 年的军队伤亡人数，一年 12 个月恰好可以将极坐标分为 12 等分，每一瓣代表一个月。图中用颜色标记出了三种死亡原因。南丁格尔的重大贡献在于使得英国政府意识到真正影响战争伤亡的并非战争本身，而是由于军队缺乏有效的医疗护理，导致大量的士兵死于可预防的疾病。1857 年，在她的努力下，英国皇家陆军卫生委员会成立。同年，军医学校成立。
1.4 拿破仑的俄罗斯远征
图 1.5: Minard 绘制的地图，展现了 1812 年拿破仑的大军团进军俄国的路线（上半部分）和撤退时的气温变化（下半部分）。这一历史事件中，法军数量的急剧减少以及恶劣的气候条件一览无遗，法国科学家 Étienne-Jules Marey 称“该图所展现出的雄辩对历史学家的笔是一种极大的挑战”
1812 年 6 月 24 日，拿破仑率领的 691,501 人的大兵团—同时也是欧洲历史上集结的最大规模的部队—开赴莫斯科。但等他们到达那里，看到的只是一座空城。城里的人都被遣散，所有的供给也被中断。由于没有正式的投降，拿破仑觉得俄国人从他那儿剥夺了一场传统意义上的胜利。
军队不得不撤退。在归程中，因为天气过于恶劣，给军队提供补给几乎是不可能的。马匹因为缺少粮草而变得虚弱，所有的马要么饿死，要么被饥饿的士兵拿去果腹。没有了坐骑，法国骑兵们成了步兵，大炮和马车被迫丢弃，部队没了装甲。饥饿与疾病带来惨重的伤亡，而逃兵数目也直线上升。大军团的小分队在 Vyazma，Krasnoi 和 Polotsk 也被俄国人击溃。法国军队在渡贝尔齐纳河时遭到俄军两面夹击，伤亡惨重，这也是法军在俄国遭遇的最后一场灾难。1812 年 12 月 14 日，大军团被驱逐出俄国领土。在这场远征俄罗斯的战役中，拿破仑的士兵只有大约 22,000 人得以幸存。
这一历史事件被 Charles Joseph Minard 用一张二维平面图形记录了下来，Minard 是一位法国工程师，他以在工程和统计中应用图形而闻名。图 1.5 就是他的著名作品：在一张二维图形中，他成功地展示了如下信息：
- 军队的位置和前进方向，以及一路上军队的分支和汇合情况
- 士兵数目的减少（图形顶端最粗的线条表示最初渡河的 422,000 人，他们一路深入到俄国领土，在莫斯科停下来的时候还有 100,000 人左右。从右到左，他们朝西走回头路，渡过 Niemen 河的时候，仅仅剩下 10,000。随着大部队和余部会师（比如在渡贝尔齐纳河之前），图中显示的数字降中也有升）
- 撤退时的气温变化（参见图的下半部分，可知当时气候条件极其恶劣）
这幅图形在统计图形界内享有至高无上的地位，被 Edward Tufte 称为“有史以来最好的统计图形”（Tufte 是统计图形和信息可视化领域的领军人物，人称“数据达芬奇”）。
1.5 小结与开始
在前面四节中，我们看到了具有历史意义的几幅统计图形，它们融入了前人的智慧与艺术，有些甚至具有重大社会价值。当然我们不能苛求每一幅统计图形都能达到那样的效果，但至少我们了解到了统计图形在揭示特殊现象或规律上的功能，这种功能是数据本身不能替代的。试想，若只是将每一个霍乱死者的数据列在纸上，那么要观察出霍乱发生的规律是何其艰难。
统计图形领域还有大批卓有成就的研究者，为统计图形的发展做出了不少贡献。在上个世纪八九十年代甚至更早，国外已经有比较全面的图示书籍文献资料，如前文提到的“数据达芬奇” Tufte，他的著作如 Tufte (1992) 和 Tufte (2001) 在可视化领域有非常深远的影响，他本人于 2010 年被奥巴马政府聘请加入“经济复苏独立咨询小组”（Recovery Independent Advisory Panel），从这一点可见他的成就和威望；但如果说统计图形有一位启蒙思想家的话，那么恐怕非 Tukey 莫属了，John. W. Tukey (1977) 提出来的探索性数据分析可以说在当时引领了一个统计学的新方向，在数理统计为主导的统计界注入了一股新活力，探索性数据分析的主要工具就是统计图形，注意 Tukey 本人的数学功底极好，这一点从若干著名统计学家的回忆录中都可以找到证据（统计学刊物 Statistical Science 每一期的最后都有一篇采访，本人在这些采访中时常见到 Tukey 被提及），但从他的一些论文著作中我们可以看到他非常重视数据分析，J. W. Tukey (1962) 就是一篇很好的例证（他认为数学不是一门科学，而数据分析则是）；Tukey 常常体现在一些细节之处展现他的观察力，令人不得不感到佩服，例如 Wainer and Thissen (1981) 中提到了一件事：过去人们常用斜线计数，\(\text{/}\) 表示 1，\(\text{//}\) 表示 2，……，达到 4 条线（\(\text{////}\)）之后紧接着用 \(\bcancel{\text{////}}\) 表示 5，但 Tukey 认为这样很容易出错，比如要是在 3 条线之后不小心早划了表示 5 的斜线 \(\bcancel{\text{///}}\)，或者在 5 条线之后才画那条反方向的斜线 \(\bcancel{\text{/////}}\)，都将造成难以修复的错误，因此他提出了一种新的计数方法：先用正方形的四个顶点分别表示 1、2、3、4，到 4 点的时候就开始连边线，每连一条线就表示数字增加 1，这样 4 条边都连好之后就可以表示到 8 了，最后分别连对角线表示 9 和 10，即 \(\boxtimes\) 表示 10，用这种计数法则不必担心画错线，因为不管连哪条线都是表示 1，其实细心的中文读者马上能联想到我们的“正”字计数法，这个计数法比 Tukey 的方法更具有稳健性；统计图形一直以来都因为缺乏像数学那样的理论而受人诟病，关于这一点，Wilkinson (2005) 则给出了一个很好的框架，它也是 R 包 ggplot2 的理论基础；贝尔实验室的的 Cleveland 在图形认知方面做了不少工作，告诉我们应该怎样合理构建图形以及解读图形，如 Cleveland (1985) 和 Cleveland (1993) 等，其中值得一提的是他可能是最早研究统计图形对读者心理感知的影响的统计学家之一，但不幸的是，这项工作似乎并没有引起人们的广泛重视（饼图直至今日仍然泛滥便是一个最好的例证），另外他提出了 S 语言中的 Trellis 图形，这对统计图形软件的发展来说也是具有划时代意义的贡献，后来 R 语言中的 lattice 包正是继承了 Trellis 图形的概念，近些年来也非常有影响力。关于统计图形的历史总结，M. Friendly and Denis (2001) 是一份非常详尽的资料，该文档整理、记载了自 17 世纪以前至今数百年历史中较有影响力的统计图形。
近代统计图形以 John. W. Tukey (1977) 的探索性数据分析为里程碑式的起点，诞生了大批具有数理统计意义和计算机应用的图形著作和图形种类，如我们熟知的箱线图 (Robert McGill and Larsen 1978)，LOWESS 曲线 (Cleveland 1979)，直方图和密度曲线 (Scott 2015)，基于 S 语言的著作 (Chambers et al. 1983) 以及注重表达信息的著作（如前文介绍的 Tufte）等；现代统计图形的发展则更偏重计算机工具的开发以及高维图形和动态图形的展示，其中 S 语言 (Becker, Chambers, and Wilks 1988) 为现代统计图形的发展奠定了重要的基础，随后 R 语言 (Ihaka and Gentleman 1996; R Core Team 2024) 的兴起，更是带来了数不胜数的统计图形方法，比较有代表性的如 R 语言的基础包 graphics 包和 grid 包 (Murrell 2018)、基于 Trellis 图形 (Cleveland 1993) 思想的 lattice 图形 (Sarkar 2008)、基于统计图形理论著作 Wilkinson (2005) 的 ggplot2 图形 (Wickham 2016)、基于动态图形 GGobi 软件 (Cook and Swayne 2007) 的高维数据交互图形实现 rggobi 包 (Wickham et al. 2018)、基于 OpenGL 的三维动态图形系统 rgl 包 (Adler and Murdoch 2024) 和分类数据图示的 vcd 包 (Meyer et al. 2023) 等，此外，还有一批新的高维图形思想被提出，如打破笛卡尔坐标系常规的平行坐标图 (Inselberg 2009)，并出现了一些 R 语言之外的独立交互图形软件如用于分析缺失值的 MANET 软件 (Unwin et al. 1996) 和交互式图形分析软件 Mondrian (Theus 2002) 等，这些动态图形和交互图形的综述可参考 Symanzik (2004)。
如今统计图形的使用看似已经比较普遍，饼图、条形图都已不是什么新鲜内容，人人都能做，但是，一方面统计图形的价值并没有被很好地体现出来，另一方面人们对统计图形的了解也被统计软件所限，而不能随心创造图形。我们来看这样一组事实 (谢益辉 2008a)：
以期刊《统计研究》在 2006 年 12 月 ~ 2007 年 11 月期间共 12 个月的所有论文作为统计对象，剔除部分非学术研究型论文之后，挑选论文总数为 168 篇，其中使用表格的论文篇数为 136 篇（81.43%），表格总数为 528 个，而使用图形的论文仅有 63 篇（37.72%），若将仅仅使用示意图（非统计图形）、条形图和折线图的论文排除在外，使用其它图形的论文仅剩下 9 篇。
这可算国内统计图形应用现状的一个缩影。为了改变这种局面、发掘出统计图形在数据分析中应有的潜力，我们特别撰写这本书，供广大统计研究者参考。我们的目的并非仅限于如何作出漂亮的统计图形，而是在作图的同时，强调图背后更重要的工作，那就是“数据分析与统计图形的有机结合”。传统的统计分析大约可以分为三类：
- 描述性统计分析：Descriptive Statistical Analysis
- 推断性统计分析：Inferential Statistical Analysis
- 探索性统计分析：Exploratory Statistical Analysis
前两类统计分析往往都是从既定的统计模型、方法的角度入手，而探索统计分析则主要借助图形对数据进行探索性分析，这对于数据分析的手段是一种重要的拓展（姑且称之为“图形统计分析”）；然而要使用这种手段，则必须清楚了解如何制图以及现有图形有哪些种类，这样才能真正开发出统计图形的价值。
其实，“图形统计分析”也不是一个新概念，平常的统计图示已经或多或少用到了这样的思想，只是我们往往更倾向于数理意义上的统计模型分析，而不会把图形统计分析作为主要分析手段。当然，由于图形的表达限制以及统计图形的普及程度，也使得它不可能替代模型分析，但无论如何，我们对统计图形在统计分析中的地位应该加深认识，不仅是因为这是一个信息爆炸的时代、大量的信息让我们无法在短时间内获取核心信息，更重要的是，目前在国内仍有大量的统计图形未被开发介绍出来，图形种类过于单一，表达信息的效果大打折扣。
本书介绍统计图形的方式主要是从两方面入手，第一，阐明各种统计图形所用到的统计量；第二，与实例结合，解释图形中表现的统计量的实际含义。在本书的附录 B 中，我们也会介绍一些有用的细节和作图技巧，用以辅助完善统计图形。
总的说来，要把图形提到“统计分析”的高度，就一定要搞清楚统计图形的来龙去脉，包括原始数据的来源和类型、统计量的计算、图形的构造与组合机制等，这与统计模型实际上没有本质的区别：若不清楚模型的假设前提、计算原理以及相应的结果解释，同样也不能随便使用模型分析。除了图形本身之外，用好图形分析还需要一定的洞察力，最简单的莫过于观察数据的分布状况、离群点、线性/非线性关系等表面观察，而更重要也是最本质的莫过于洞察到种种规律或异常现象背后的深刻原因，至此，我们才达到了分析的目的。
1.6 思考与练习
图 1.1 的主旨是用来刻画贸易顺差或逆差，因此把出口额和进口额画在同一幅图上似乎是自然而然的选择，但是我们真正关心的是两条曲线之差。你认为 Playfair 的这幅图是否存在不足、以及应该怎样改进？
某种程度上，Tukey 引导了“用数据说话”的潮流，这样的做法有什么潜在危险？换句话说，当我们浏览一幅图形的时候，我们首先要考虑的是数据的来源，如果我们忽略数据的来源而直接去考虑基于图形的发现，所谓的“数据说的话”是什么话？
统计图形和统计模型的最大区别在哪里？提示：并非高下之分，而是二者各自的假设是什么。更具体地，我们知道数理统计中的假设检验通常有零假设和备择假设，统计图形更像在研究哪一个假设，而统计模型又通常研究哪一个？