21 时序数据分析
预测是非常古老的话题,几乎人人都想拥有预测未来的能力,唐朝袁天罡和李淳风的故事至今还广为流传。事实上,古时候只有至高无上的皇帝才可以去问钦天监了解星辰大海和国运命脉。时间序列数据的分析,以及根据分析得到的一般规律进行预测是经久不衰的命题。预测既包含一般规律指向的确定性,又有无法预知的不确定性,且同时包含认知局限带来的不确定性,后者往往更大。无休止地渴求往往伴随着巨大的挑战,而更大的挑战则是预测效果常常不能满足期待。
本章主要从以下几个方面展开:数据获取、数据探索、平稳性诊断、时间序列分解、模型拟合和预测。
21.1 数据获取
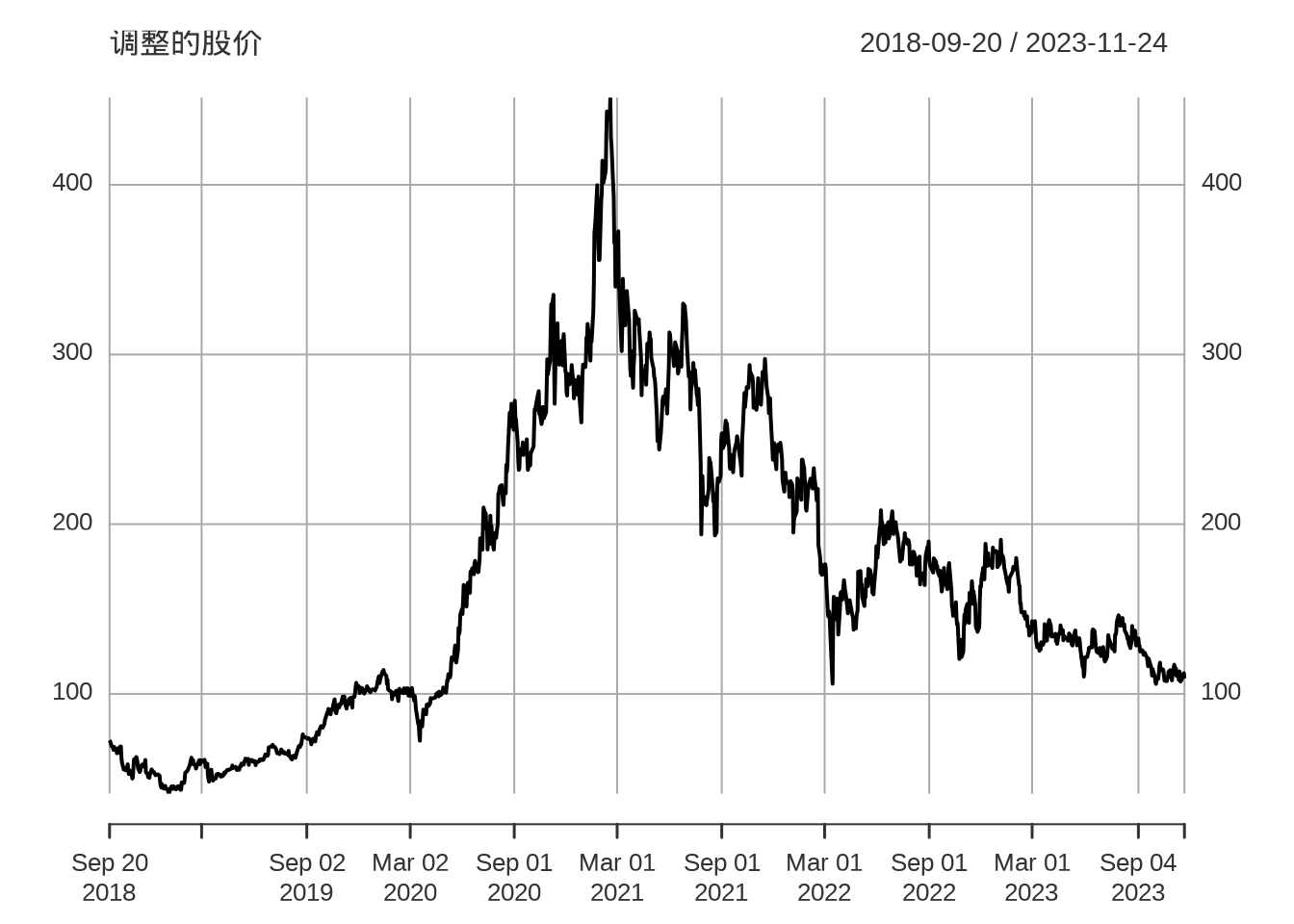
Joshua M. Ulrich 开发维护的 quantmod 包可以下载国内外股票市场的数据。本节主要以美团股价数据为例,美团自 2018-09-20 在香港挂牌上市,股票代码 3690.HK。首先用 quantmod 包 (Ryan 和 Ulrich 2022) 获取美团上市至 2023-11-24 每天的股价数据,包含 Open 开盘价、High 最高价、Low 最低价、Close 闭市价、Adjusted 调整价和 Volume 成交量数据。
先来看数据的类型,数据类型颇为复杂,是由 xts 和 zoo 两种类型复合而成,xts 类型是继承自 zoo 类型的。
[1] "xts" "zoo"An xts object on 2018-09-20 / 2023-11-24 containing:
Data: double [1275, 6]
Columns: 3690.HK.Open, 3690.HK.High, 3690.HK.Low, 3690.HK.Close, 3690.HK.Volume ... with 1 more column
Index: Date [1275] (TZ: "UTC")
xts Attributes:
$ src : chr "yahoo"
$ updated: POSIXct[1:1], format: "2023-11-27 06:31:12"数据集 meituan 是一个 xts 类型的时间序列数据对象,时间范围是 2018-09-20 至 2023-11-24,包含 4 个成分,分别如下
- Data 部分显示为 906 行 6 列的双精度浮点存储的数值。
- Columns 部分显示列名,依次是 3690.HK.Open、3690.HK.High、 3690.HK.Low 和 3690.HK.Close 等,当列数很多时,显示时会省略。
- Index 部分表示索引列,有序是时间序列数据的本质特点。示例中索引存储数据点产生的先后顺序,索引是用日期来表示的,日期所在的时区是 “UTC”。
- xts 部分是数据类型的一些属性(元数据),说明数据集的来源,什么时候制作的数据。示例中数据是从雅虎财经下载的,下载时间是 2023-11-27 14:31:12。
与时间序列数据相关的数据类型有很多,比如 Base R 提供的 Date 和 POSIX 等,扩展包 timeDate 和 chron 也都有自己的一套数据类型及处理方法。xts 包是处理时间序列数据的主要工具之一,xts 是 eXtensible Time Series 的缩写。为了进一步了解用法,下面举个例子,使用该 R 包的函数 xts() 构造时间序列对象。
- 参数
x表示数据。 - 参数
order.by表示索引数据。 - 参数
frequency表示频率。 - 参数
unique表示唯一。 - 参数
tzone表示时区。
21.2 数据探索
21.2.1 zoo
zoo 包提供 S3 范型函数 autoplot.zoo() 专门可视化 zoo 类型的数据,它接受一个 zoo 类型的数据对象,返回一个 ggplot2 数据对象,然后用户可以添加自定义的绘图设置,更多详情见帮助文档 ?autoplot.zoo() 。
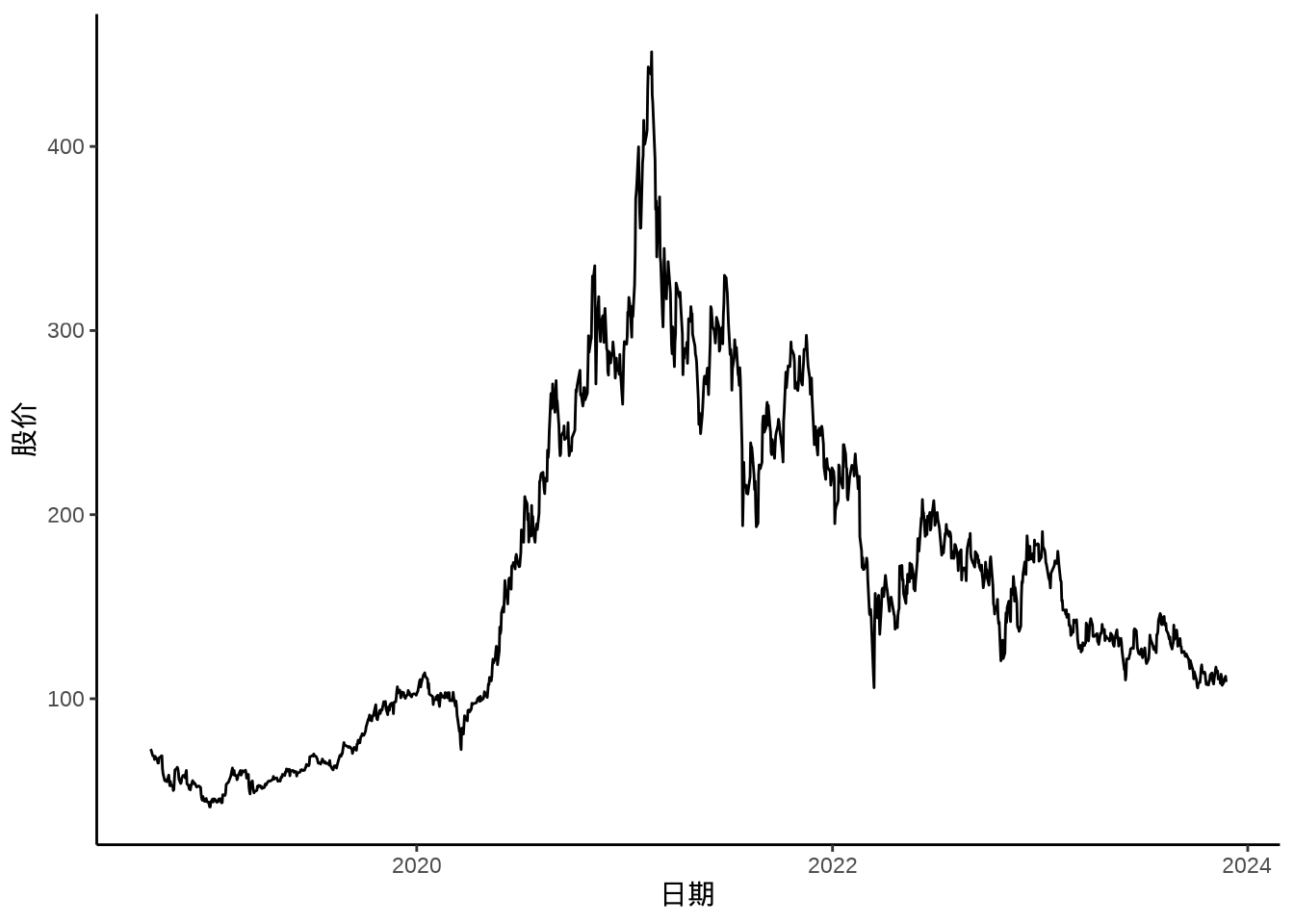
zoo 包还提供另一个范型函数 fortify() 将 zoo 数据对象转化为 data.frame ,这可以方便使用 ggplot2 包来展示数据。参数 melt = TRUE 意味着重塑原数据集,将数据从宽格式转长格式。参数 names = c(Index = "Date") 表示将 Index 列重命名为 date 列。
数据集 meituan_df 中的 Series 列是因子型的,将其标签 3690.HK.Adjusted 、3690.HK.High 调整为调整价、最高价。根据日期字段 Date 提取年份字段 year 和一年中的第几天的字段 day_of_year。
调用 ggplot2 包绘制分面、分组时间序列图,以 day_of_year 为横轴,股价 Value 为纵轴,按 year 分组,按 Series 分面。
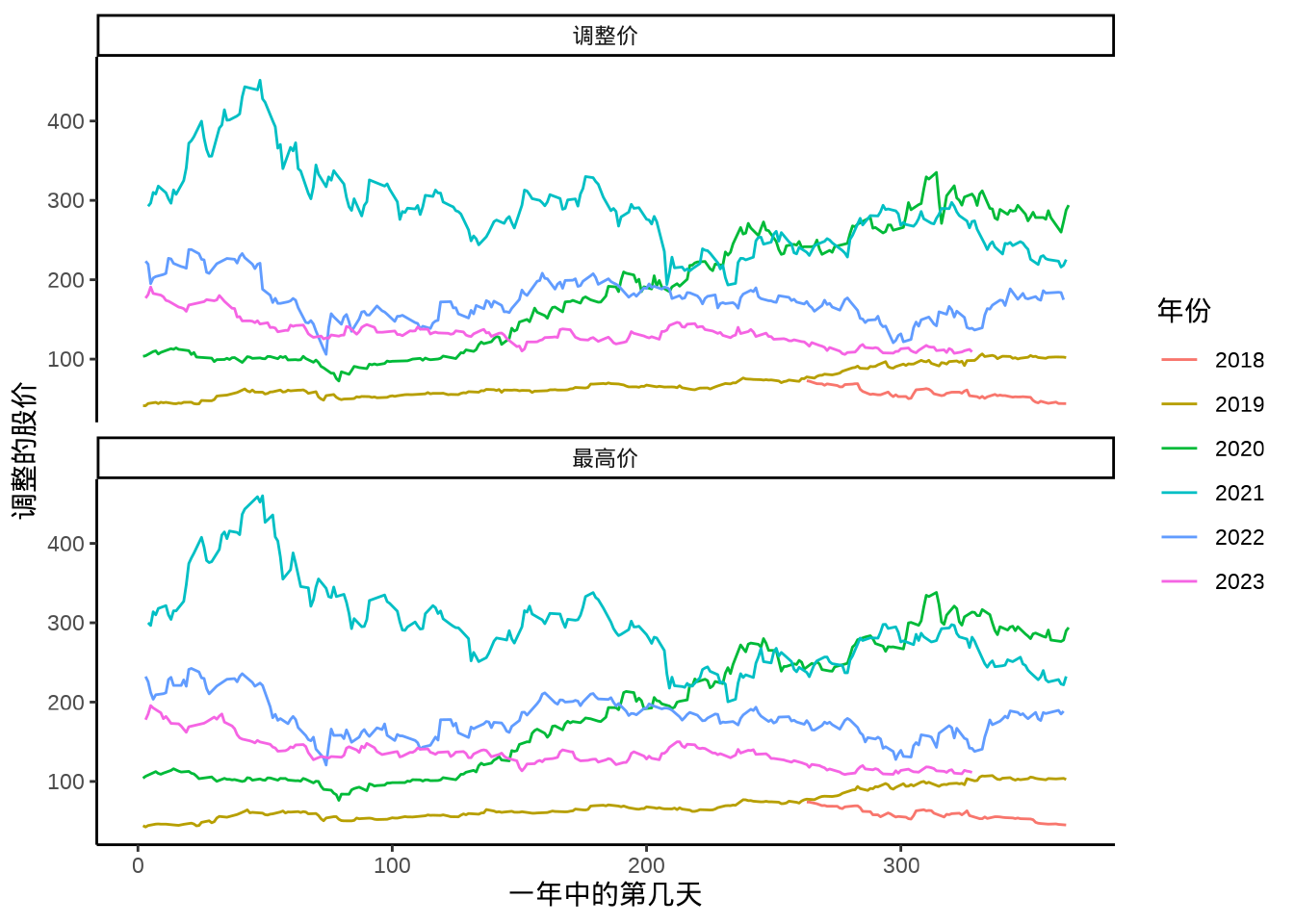
2019 年底开始出现疫情,2020 年整年陆续有疫情,美团股价一路狂飙突进,因疫情,利好外卖业务,市场看好外卖业务。2021 年政府去杠杆,互联网监管趋严,又监又管,受外部大环境,逆全球化趋势影响,整年股价一路走低。进入 2022 年,股价在 200 附近徘徊。
21.2.2 xts
xts 包提供 S3 泛型函数 plot.xts() 专门用来可视化 xts 类型的时间序列数据
还可以任意选择一个时间窗口,展示相关数据
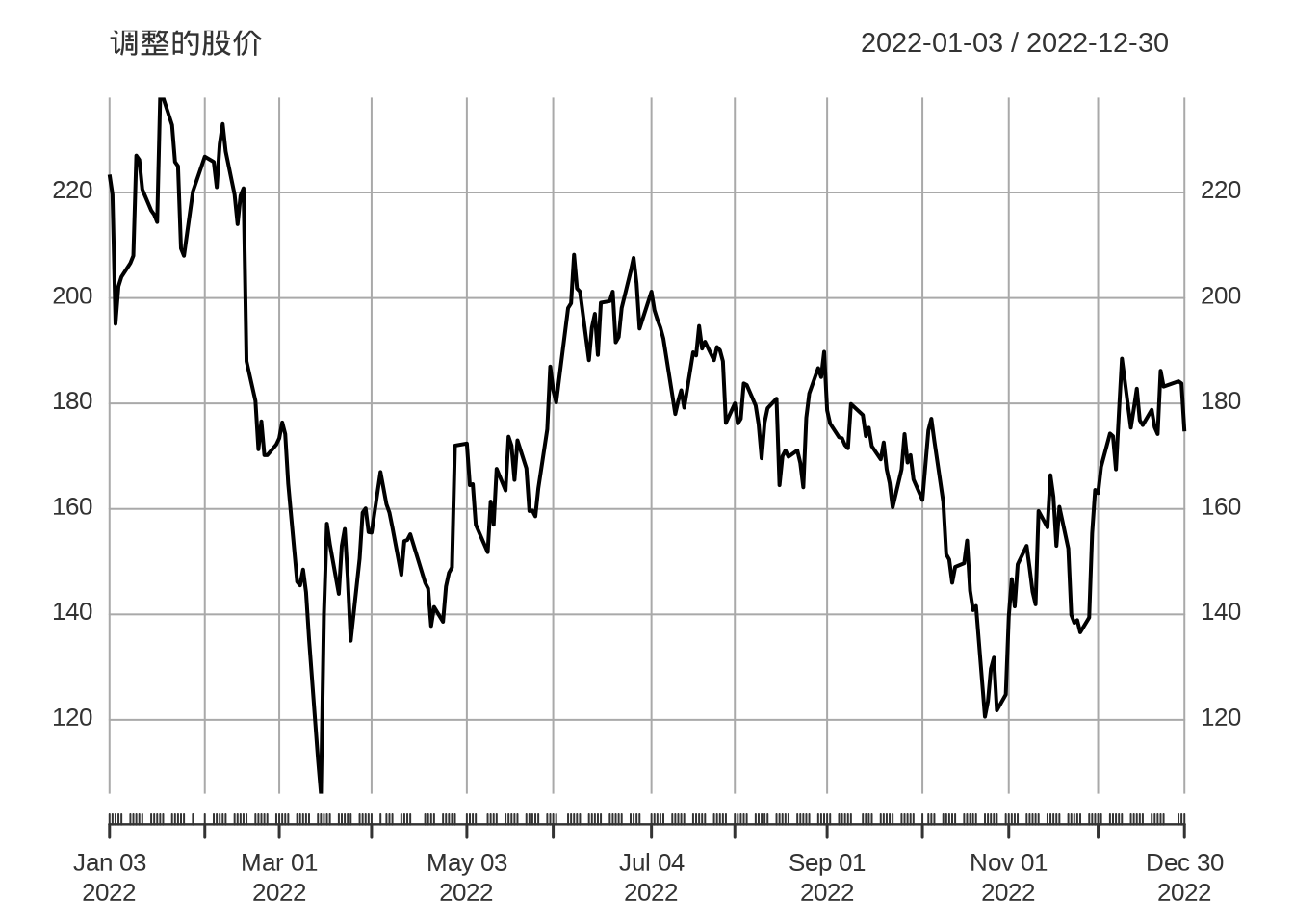
元旦节三天不开市,所以假期没有数据。
21.2.3 ggfortify
ggfortify (Tang, Horikoshi, 和 Li 2016) 支持快速地可视化 ts、timeSeries 、stl 等多种类型的时序数据, ggplot2 做数据探索会有一些帮助。
Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
ℹ Please use tidy evaluation idioms with `aes()`.
ℹ See also `vignette("ggplot2-in-packages")` for more information.
ℹ The deprecated feature was likely used in the ggfortify package.
Please report the issue at <https://github.com/sinhrks/ggfortify/issues>.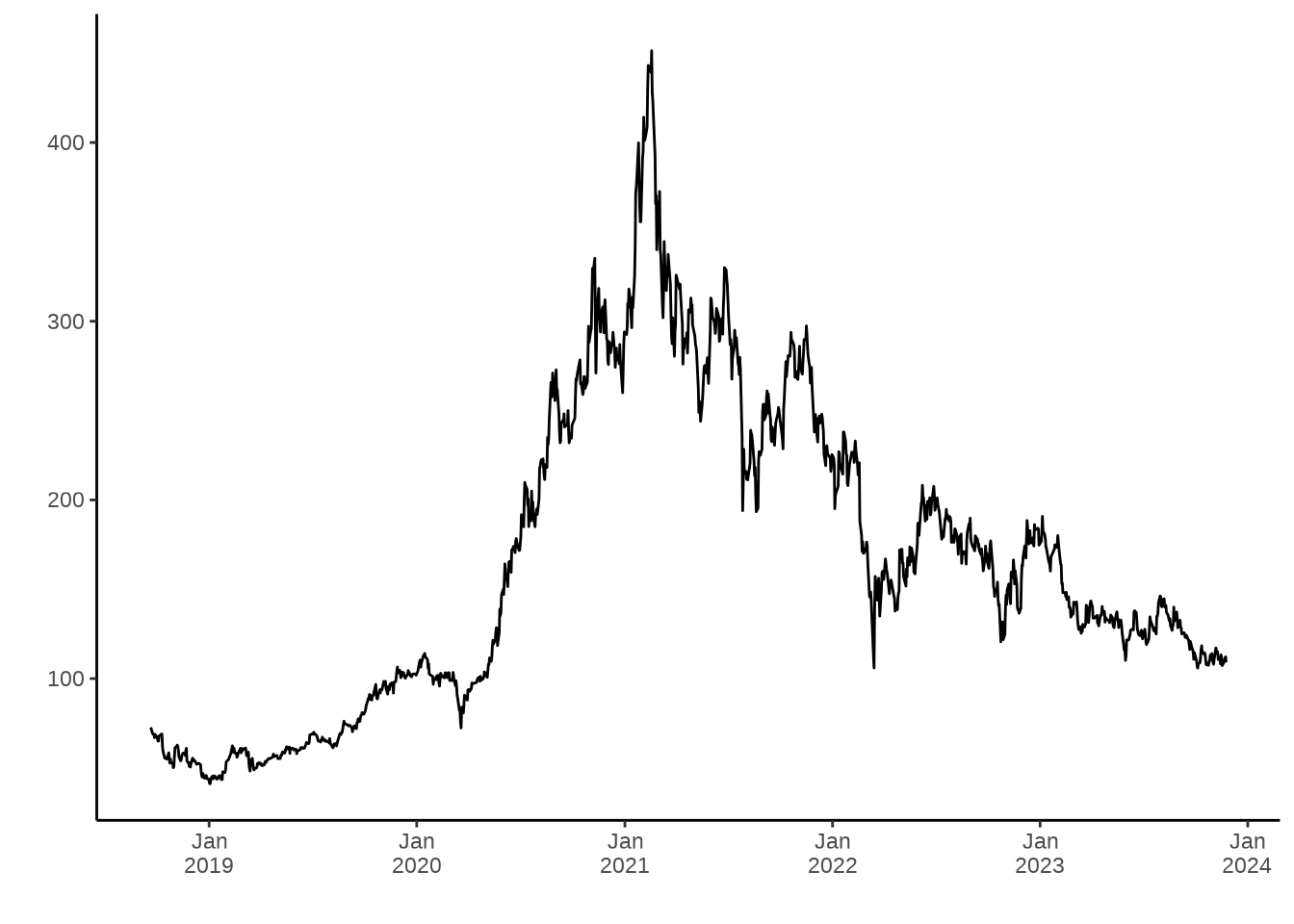
21.2.4 dygraphs
dygraphs 包专门绘制交互式时间序列图形,它封装了时序数据可视化库 dygraphs ,更多情况见 https://dygraphs.com/。下面以美团股价为例,展示时间窗口筛选、坐标轴名称、刻度标签、注释、事件标注、缩放等功能。
library(dygraphs)
# 缩放
dyUnzoom <- function(dygraph) {
dyPlugin(
dygraph = dygraph,
name = "Unzoom",
path = system.file("plugins/unzoom.js", package = "dygraphs")
)
}
# 年月
getYearMonth <- '
function(d) {
var monthNames = ["01", "02", "03", "04", "05", "06","07", "08", "09", "10", "11", "12"];
date = new Date(d);
return date.getFullYear() + "-" + monthNames[date.getMonth()];
}'
# 绘图
dygraph(meituan[, "3690.HK.Adjusted"], main = "美团股价走势") |>
dyRangeSelector(dateWindow = c("2023-01-01", "2023-11-24")) |>
dyAxis(name = "x", axisLabelFormatter = getYearMonth) |>
dyAxis("y", valueRange = c(0, 500), label = "美团股价") |>
dyEvent("2020-01-23", "武汉封城", labelLoc = "bottom") |>
dyShading(from = "2020-01-23", to = "2020-04-08", color = "#FFE6E6") |>
dyAnnotation("2020-01-23", text = "武汉封城", tooltip = "武汉封城", width = 60) |>
dyAnnotation("2020-04-08", text = "武汉解封", tooltip = "武汉解封", width = 60) |>
dyHighlight(highlightSeriesOpts = list(strokeWidth = 2)) |>
dySeries(label = "调整股价") |>
dyLegend(show = "follow", hideOnMouseOut = FALSE) |>
dyOptions(fillGraph = TRUE, drawGrid = FALSE, gridLineColor = "lightblue") |>
dyUnzoom()上图默认展示 YTD 数据,在一个动态的时间窗口内显示数据,假如今天是 2023-07-15,则展示 2023-01-01 至 2023-07-15 的股价数据。在函数 dyRangeSelector() 中设定时间窗口参数 dateWindow,实现数据范围的筛选。
21.3 平稳性诊断
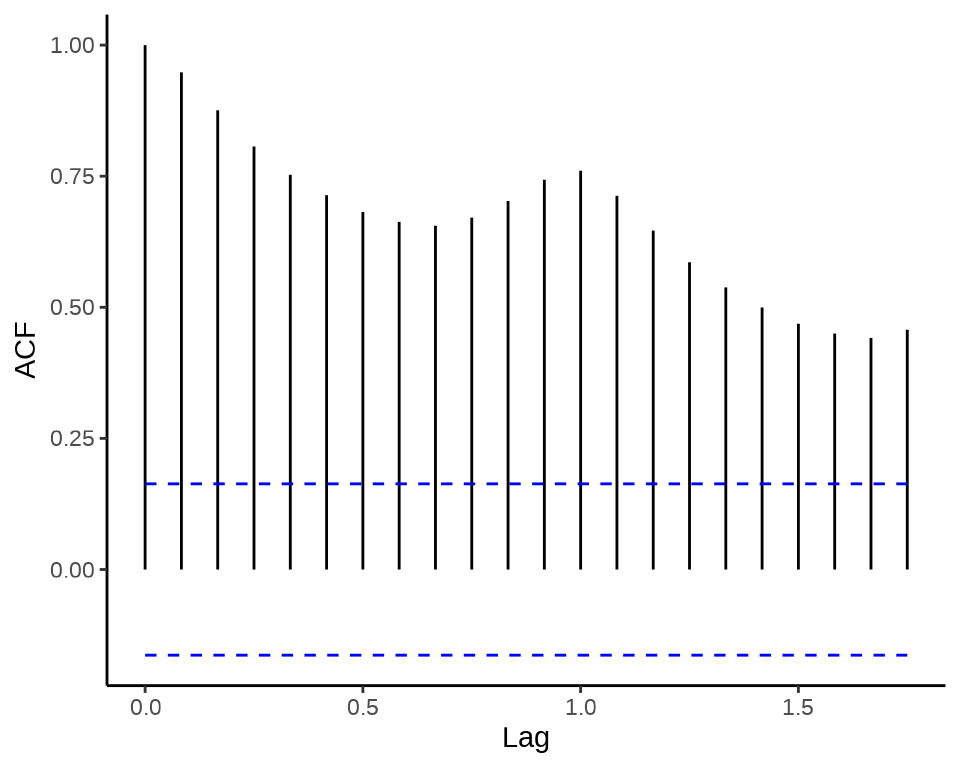
21.3.1 自相关图
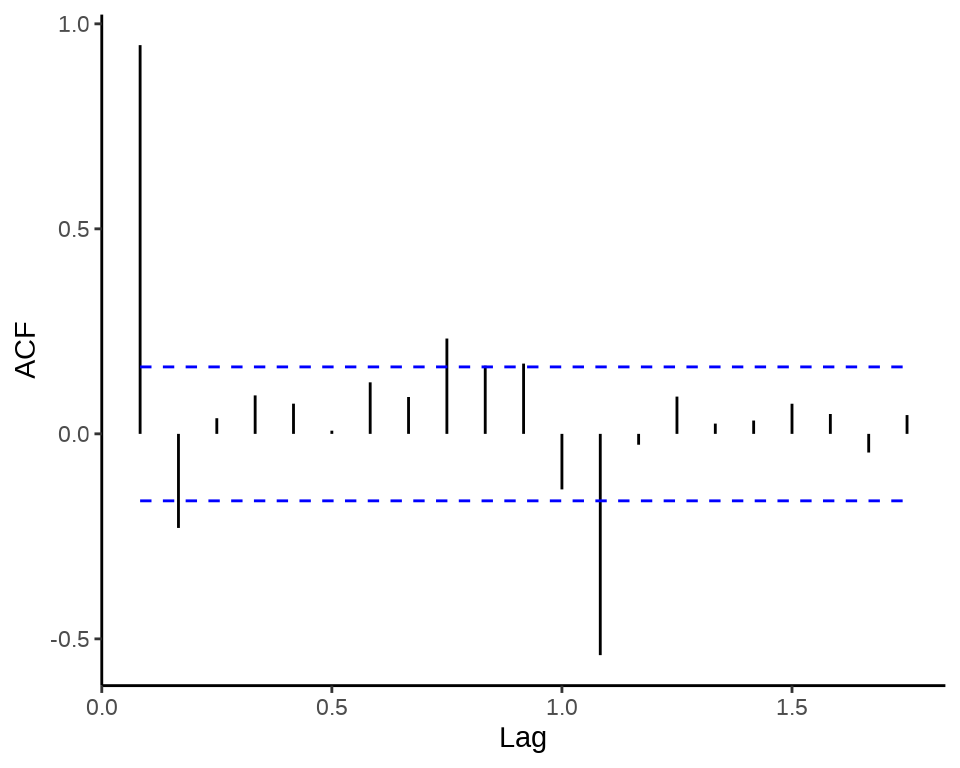
21.3.2 偏自相关图
21.3.3 延迟算子
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
1952 171 180 193 181 183 218 230 242 209 191 172 194
1953 196 196 236 235 229 243 264 272 237 211 180 201
1954 204 188 235 227 234 264 302 293 259 229 203 229
1955 242 233 267 269 270 315 364 347 312 274 237 278
1956 284 277 317 313 318 374 413 405 355 306 271 306
1957 315 301 356 348 355 422 465 467 404 347 305 336
1958 340 318 362 348 363 435 491 505 404 359 310 337
1959 360 342 406 396 420 472 548 559 463 407 362 405
1960 417 391 419 461 472 535 622 606 508 461 390 432 Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1948 112
1949 118 132 129 121 135 148 148 136 119 104 118 115
1950 126 141 135 125 149 170 170 158 133 114 140 145
1951 150 178 163 172 178 199 199 184 162 146 166 171
1952 180 193 181 183 218 230 242 209 191 172 194 196
1953 196 236 235 229 243 264 272 237 211 180 201 204
1954 188 235 227 234 264 302 293 259 229 203 229 242
1955 233 267 269 270 315 364 347 312 274 237 278 284
1956 277 317 313 318 374 413 405 355 306 271 306 315
1957 301 356 348 355 422 465 467 404 347 305 336 340
1958 318 362 348 363 435 491 505 404 359 310 337 360
1959 342 406 396 420 472 548 559 463 407 362 405 417
1960 391 419 461 472 535 622 606 508 461 390 432 21.3.4 差分算子
函数 diff() 实现差分算子,默认参数 lag = 1 ,differences = 1 表示延迟期数为 1 的一阶差分。
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 6 14 -3 -8 14 13 0 -12 -17 -15 14
1950 -3 11 15 -6 -10 24 21 0 -12 -25 -19 26
1951 5 5 28 -15 9 6 21 0 -15 -22 -16 20
1952 5 9 13 -12 2 35 12 12 -33 -18 -19 22
1953 2 0 40 -1 -6 14 21 8 -35 -26 -31 21
1954 3 -16 47 -8 7 30 38 -9 -34 -30 -26 26
1955 13 -9 34 2 1 45 49 -17 -35 -38 -37 41
1956 6 -7 40 -4 5 56 39 -8 -50 -49 -35 35
1957 9 -14 55 -8 7 67 43 2 -63 -57 -42 31
1958 4 -22 44 -14 15 72 56 14 -101 -45 -49 27
1959 23 -18 64 -10 24 52 76 11 -96 -56 -45 43
1960 12 -26 28 42 11 63 87 -16 -98 -47 -71 4221.3.5 单位根检验
21.3.6 格兰杰因果检验
1969 年 Clive Granger 提出格兰杰因果检验,R 语言中 lmtest 包的函数 grangertest() 可以检验序列中变量之间的时间落差的相关性。
21.4 指数平滑模型
21.4.1 指数平滑
首先来回答何为指数平滑?用历史数据的线性组合预测下一个时期的值,线性组合的权重随距离变远而按指数衰减。不妨设观测序列数据为 \(\{x_i\}\) ,预测序列数据为 \(\{y_i\}\),用数学公式表达,如下:
\[ y_h(1) = wx_h + w^2x_{h-1} + \cdots = \sum_{j=1}^{\infty} w^j x_{h+1-j} \]
其中,权重 \(0 < w < 1\) ,权重越小表示距离远的历史数据对当前预测的贡献越小。线性组合的权重之和等于 1,所以
\[ \sum_{j=1}^{\infty} w^j = \frac{w}{1-w} \]
则第 \(j\) 个权重应为
\[ \frac{w^j}{\frac{w}{1-w}} = (1-w)w^{j-1},j=1,2,\ldots \]
则根据历史的 \(h\) 期数据预测未来的 1 期数据 \(y_h(1)\) 如下:
\[ y_h(1) = (1-w)(x_h + wx_{h-1} + w^2x_{h-2} + \cdots) = (1-w)\sum_{j=0}^{\infty}w^j x_{h-j} \]
以上就是指数平滑(exponential smoothing),在早期应用中,权重 \(w\) 的选取主要依靠经验。适用于没有明显趋势性、季节性、周期性的时间序列数据。
21.4.2 函数 filter()
函数 filter() 实现一元时间序列的线性过滤,或者对多元时间序列的单个序列分别做线性变换,它只是根据既定的平滑模型变换数据,没有拟合数据。函数 filter() 实现递归过滤和卷积过滤两种数据变换方式,分别对应自回归和移动平均两种时间序列平滑模型。
- 递归过滤(自回归)
\[ y_{i} = x_{i} + f_1 y_{i-1} +\cdots+ f_p y_{i-p} \tag{21.1}\]
- 卷积过滤(移动平均)
\[ y_{i} = f_1 x_{i+o} + \cdots + f_p x_{i+o-(p-1)} \tag{21.2}\]
其中,\(p\) 代表模型的阶数, \(o\) 代表漂移项,O 表示英文单词 offset 的首字母。下面举个具体的例子来说明函数 filter() 的作用,设输入序列 \(\{x_i\}\) 是从 1 至 10 的整数。首先考虑自回归的情况,代码如下:
Time Series:
Start = 1
End = 10
Frequency = 1
[1] 1.000000 2.666667 4.944444 7.907407 11.540123 15.835391 20.798182
[8] 26.428041 32.724289 39.687230参数 x 指定输入的时间序列 \(\{x_i\}\),参数 method 指定平滑的方法,method = "recursive" 表示使用自回归方法,参数 filter 表示自回归的系数,系数向量的长度代表模型 式 21.1 中的 \(p\) ,filter = c(2 / 3, 1 / 6, 1 / 6) 对应的模型如下:
\[ \begin{aligned} y_1 &= x_1 \\ y_2 &= x_2 + \frac{2}{3} y_1 \\ y_3 &= x_3 + \frac{2}{3} y_2 + \frac{1}{6} y_1 \\ y_i &= x_i + \frac{2}{3} y_{i-1} + \frac{1}{6} y_{i - 2} + \frac{1}{6} y_{i - 3}, \quad i \geq 4 \\ \end{aligned} \]
其中,序列 \(\{y_i\}\) 表示函数 filter() 的输出结果,由上述方程不难看出自回归模型的递归的特点。为了理解自回归和递归的过程,下面依次计算 \(y_1\) 至 \(y_4\) 。
[1] 1[1] 2.666667[1] 4.944444[1] 7.907407接下来,考虑移动平均的情况,代码如下:
Time Series:
Start = 1
End = 10
Frequency = 1
[1] NA NA 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5参数 method = "convolution" 表示使用移动平均。参数 sides 仅适用于卷积过滤,sides = 1 表示系数都是作用于过去的值。为了对比自回归和移动平均,不妨设移动平均的系数同自回归的系数,则移动平均模型如下:
\[ \begin{aligned} y_1 &~~ \text{不存在}\\ y_2 &~~ \text{不存在}\\ y_3 &= \frac{2}{3} x_{3} + \frac{1}{6} x_2 + \frac{1}{6} x_1\\ y_i &= \frac{2}{3} x_{i} + \frac{1}{6} x_{i - 1} + \frac{1}{6} x_{i - 2}, \quad i \geq 3 \end{aligned} \]
比照模型 式 21.2 ,漂移项参数 \(o\) 为 0,也就是没有漂移,移动平均作用于过去的 3 期数据,也就是 \(p = 3\) 。因输出序列 \(\{y_i\}\) 中 \(y_1,y_2\) 不存在,下面仅计算 \(y_3,y_4\) 。
TTR 包提供许多移动平均的计算函数,比如 SMA() ,下面计算过去 3 个观察值的算术平均。
21.4.3 简单指数平滑
当时间序列不含趋势和季节性成分的时候,可以用简单指数平滑模型来拟合和预测。简单指数平滑模型如下:
\[ \begin{aligned} \hat{y}_{t+h} &= a_{t} + h \times b_{t} + s_{t - p + 1 + (h - 1) \mod p} \\ a_{t} &= \alpha (y_{t} - s_{t-p}) + (1-\alpha) (a_{t-1} + b_{t-1}) \\ b_{t} &= b_{t-1} \\ s_{t} &= s_{t-p} \end{aligned} \]
其中,周期 \(p\)
Holt-Winters exponential smoothing without trend and without seasonal component.
Call:
HoltWinters(x = AirPassengers, beta = FALSE, gamma = FALSE)
Smoothing parameters:
alpha: 0.9999339
beta : FALSE
gamma: FALSE
Coefficients:
[,1]
a 431.9972预测的残差平方和 SSE sum-of-squared-errors
Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_line()`).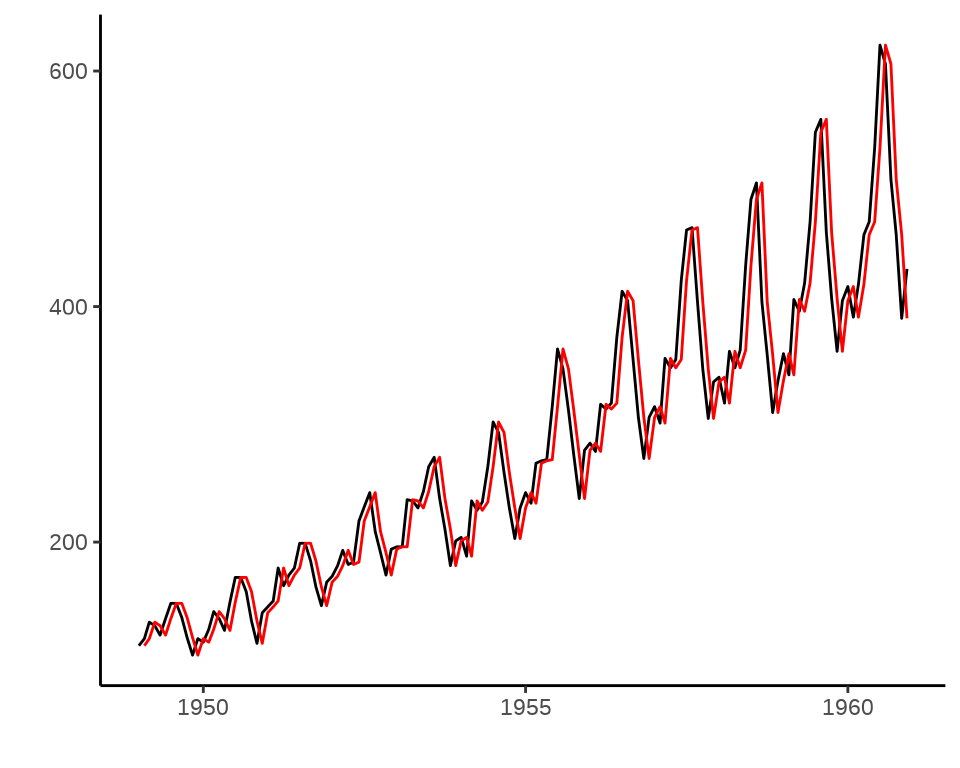
向前预测 5 期
预测值及其预测区间
21.4.4 Holt 指数平滑
当时间序列不含季节性成分,可以用 Holt 指数平滑模型拟合和预测 (Holt 2004) 。
\[ \begin{aligned} \hat{y}_{t+h} &= a_{t} + h \times b_{t} + s_{t - p + 1 + (h - 1) \mod p} \\ a_{t} &= \alpha (y_{t} - s_{t-p}) + (1-\alpha) (a_{t-1} + b_{t-1}) \\ b_{t} &= \beta (a_{t} - a_{t-1}) + (1-\beta) b_{t-1} \\ s_{t} &= s_{t-p} \end{aligned} \]
Warning in HoltWinters(AirPassengers, gamma = FALSE): optimization
difficulties: ERROR: ABNORMAL_TERMINATION_IN_LNSRCHHolt-Winters exponential smoothing with trend and without seasonal component.
Call:
HoltWinters(x = AirPassengers, gamma = FALSE)
Smoothing parameters:
alpha: 1
beta : 0.003218516
gamma: FALSE
Coefficients:
[,1]
a 432.000000
b 4.597605可知,\(\alpha = 1,\beta = 0.0032\)
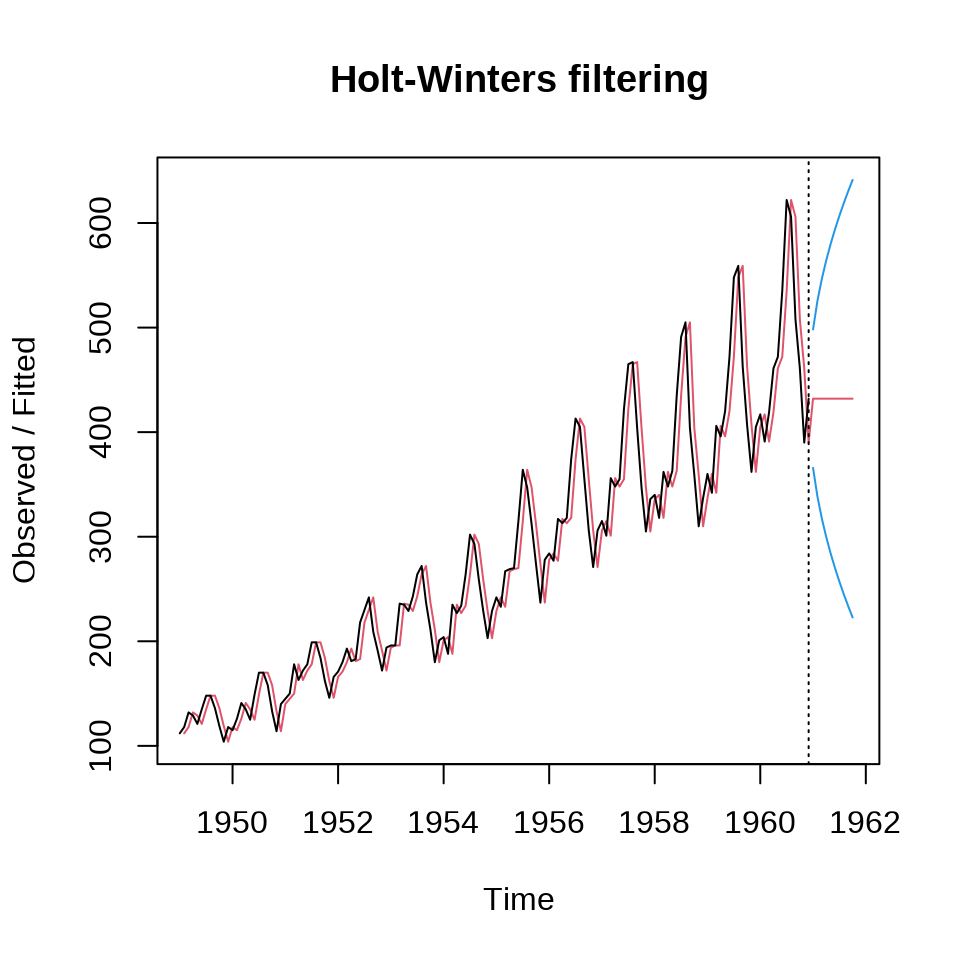
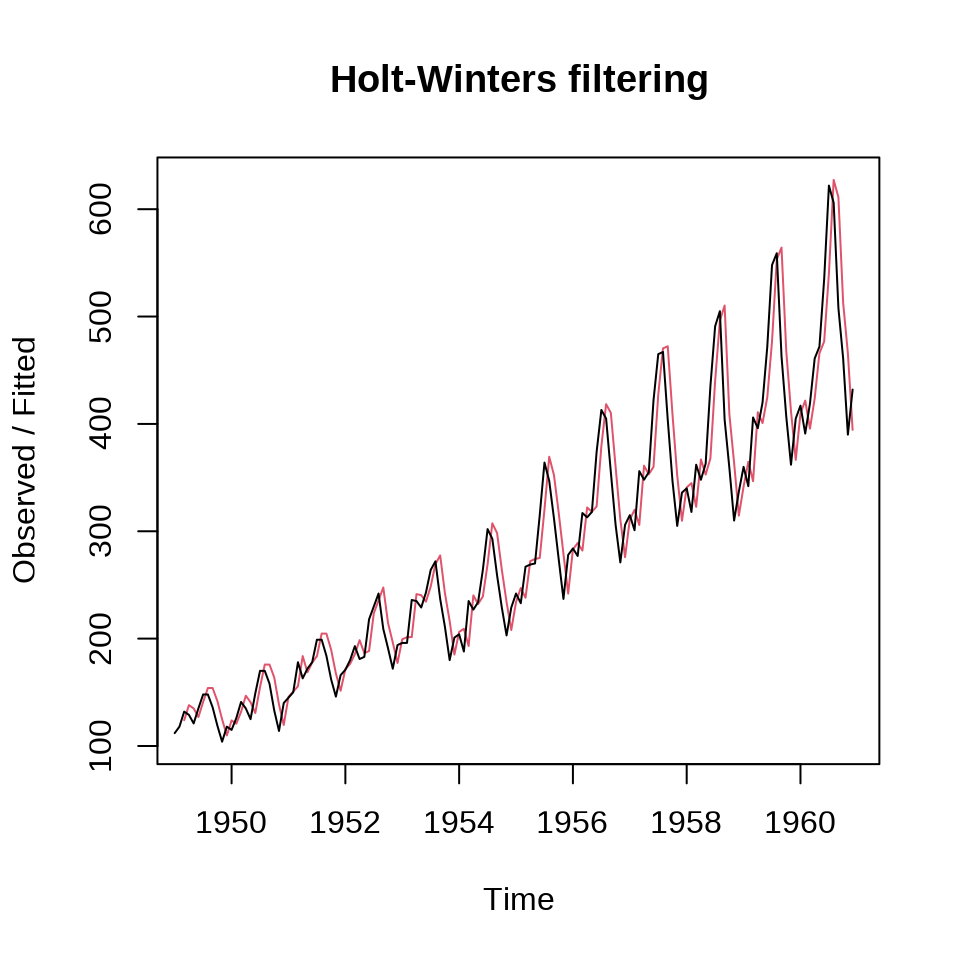
21.4.5 Holt-Winters 指数平滑
时间序列同时含有趋势成分、季节性成分、随机成分,可以用 Holt-Winters 平滑模型来拟合和预测。根据趋势和季节性的关系,Holt-Winters 平滑模型分为可加 Holt-Winters 平滑和可乘 Holt-Winters 平滑。R 提供函数 HoltWinters() 拟合 Holt-Winters 平滑模型(Holt 2004; Winters 1960)。
可加 Holt-Winters 平滑模型如下:
\[ \begin{aligned} \hat{y}_{t+h} &= a_{t} + h \times b_{t} + s_{t - p + 1 + (h - 1) \mod p} \\ a_{t} &= \alpha (y_{t} - s_{t-p}) + (1-\alpha) (a_{t-1} + b_{t-1}) \\ b_{t} &= \beta (a_{t} - a_{t-1}) + (1-\beta) b_{t-1} \\ s_{t} &= \gamma (y_{t} - a_{t}) + (1-\gamma) s_{t-p} \end{aligned} \]
可乘 Holt-Winters 平滑模型如下:
\[ \begin{aligned} \hat{y}_{t+h} &= (a_{t} + h \times b_{t}) \times s_{t - p + 1 + (h - 1) \mod p} \\ a_{t} &= \alpha (y_{t} / s_{t-p}) + (1-\alpha) (a_{t-1} + b_{t-1}) \\ b_{t} &= \beta (a_{t} - a_{t-1}) + (1-\beta) b_{t-1} \\ s_{t} &= \gamma (y_{t} / a_{t}) + (1-\gamma) s_{t-p} \end{aligned} \]
其中 \(\alpha, \beta, \gamma\) 是参数,\(p\) 为周期长度,\(a_{t}, b_{t}, s_{t}\) 分别代表水平、趋势和季节性成分。
Holt-Winters exponential smoothing with trend and additive seasonal component.
Call:
HoltWinters(x = AirPassengers, seasonal = "additive")
Smoothing parameters:
alpha: 0.2479595
beta : 0.03453373
gamma: 1
Coefficients:
[,1]
a 477.827781
b 3.127627
s1 -27.457685
s2 -54.692464
s3 -20.174608
s4 12.919120
s5 18.873607
s6 75.294426
s7 152.888368
s8 134.613464
s9 33.778349
s10 -18.379060
s11 -87.772408
s12 -45.827781可知,\(\alpha = 0.248,\beta = 0.0345,\gamma = 1\)
Warning: Removed 12 rows containing missing values or values outside the scale range
(`geom_line()`).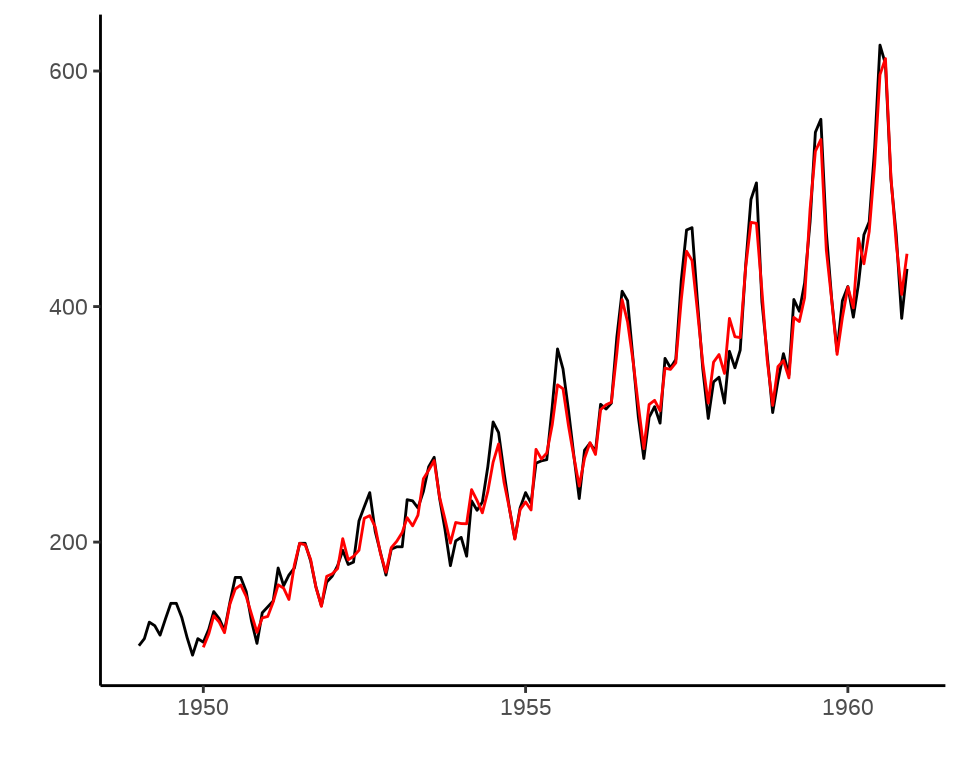
Warning: Removed 12 rows containing missing values or values outside the scale range
(`geom_line()`).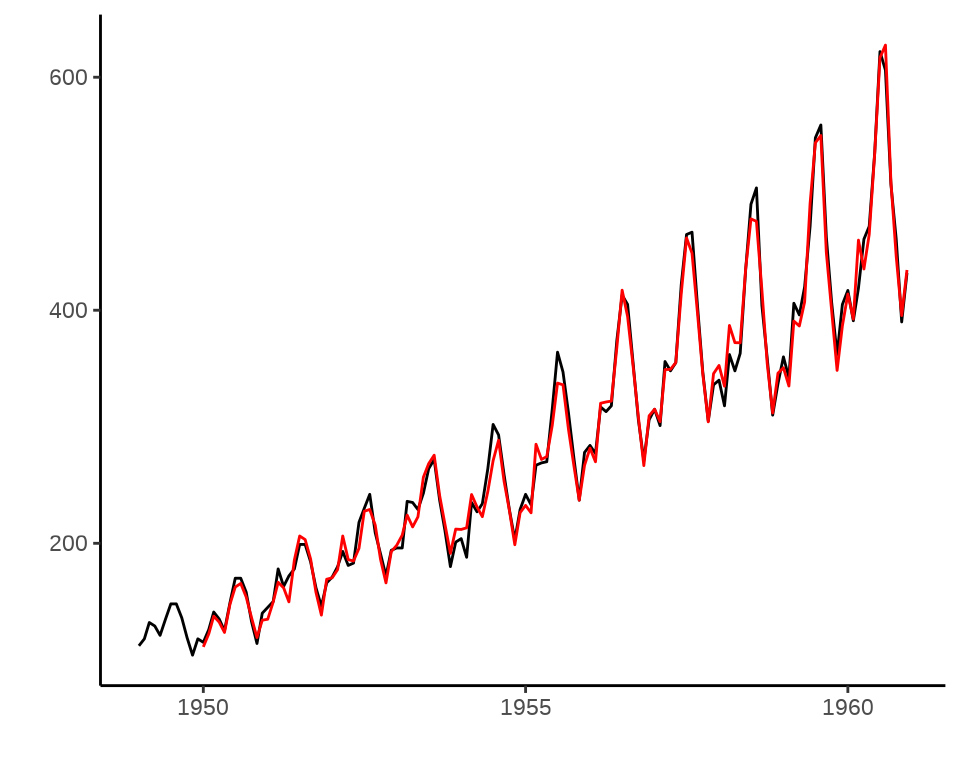
做一个 Shiny 应用展示参数 \(\alpha, \beta, \gamma\) 对 Holt-Winters 平滑预测的影响。
21.5 时间序列分解
- 可加模型
\[ y_t = T_t + S_t + e_t \]
- 可乘模型
\[ y_t = T_t \times S_t \times e_t \]
对时间序列 \(\{y_t\}\) 分解,趋势性成分 \(T_t\)、季节性成分 \(S_t\)、剩余成分 \(e_t\)
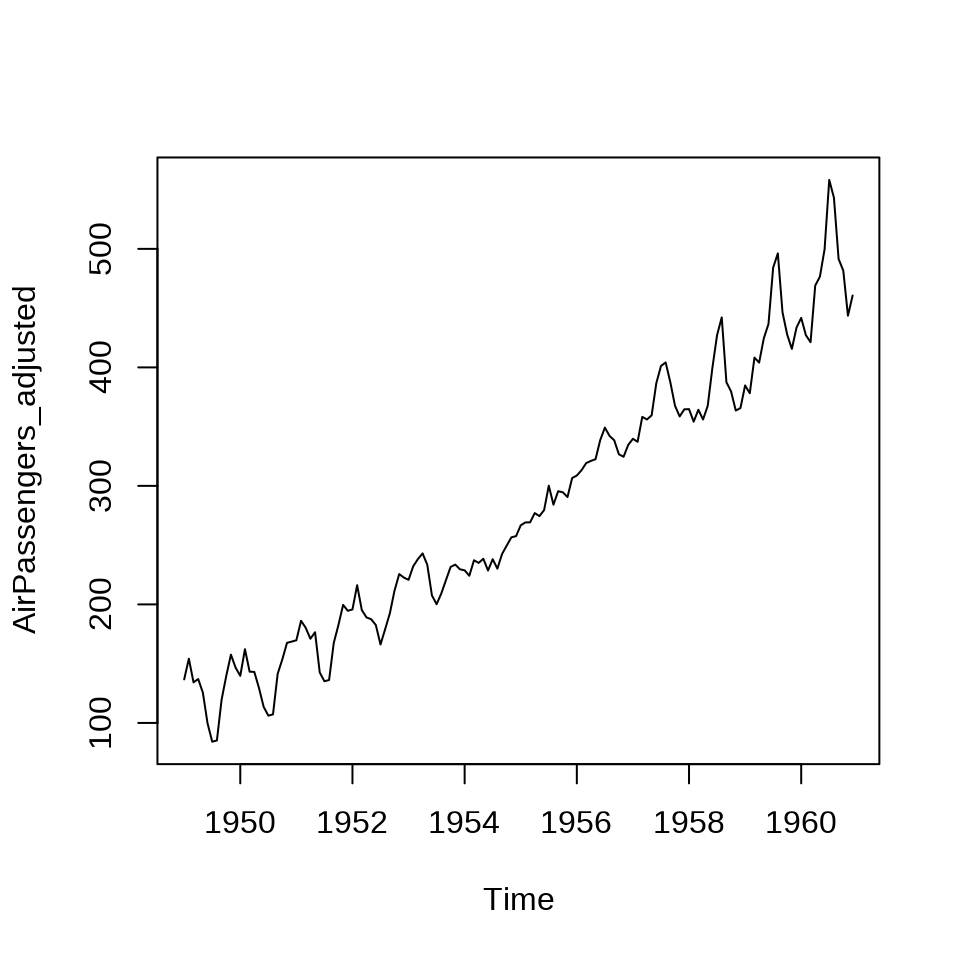
21.5.1 函数 decompose()
函数 decompose() 分解
函数返回一个列表,包含 6 个元素,分别是 x 原始序列,seasonal 季节性成分,figure 估计的季节图,trend 趋势成分,random 剩余成分,type 分解方法。
Warning: Removed 24 rows containing missing values or values outside the scale range
(`geom_line()`).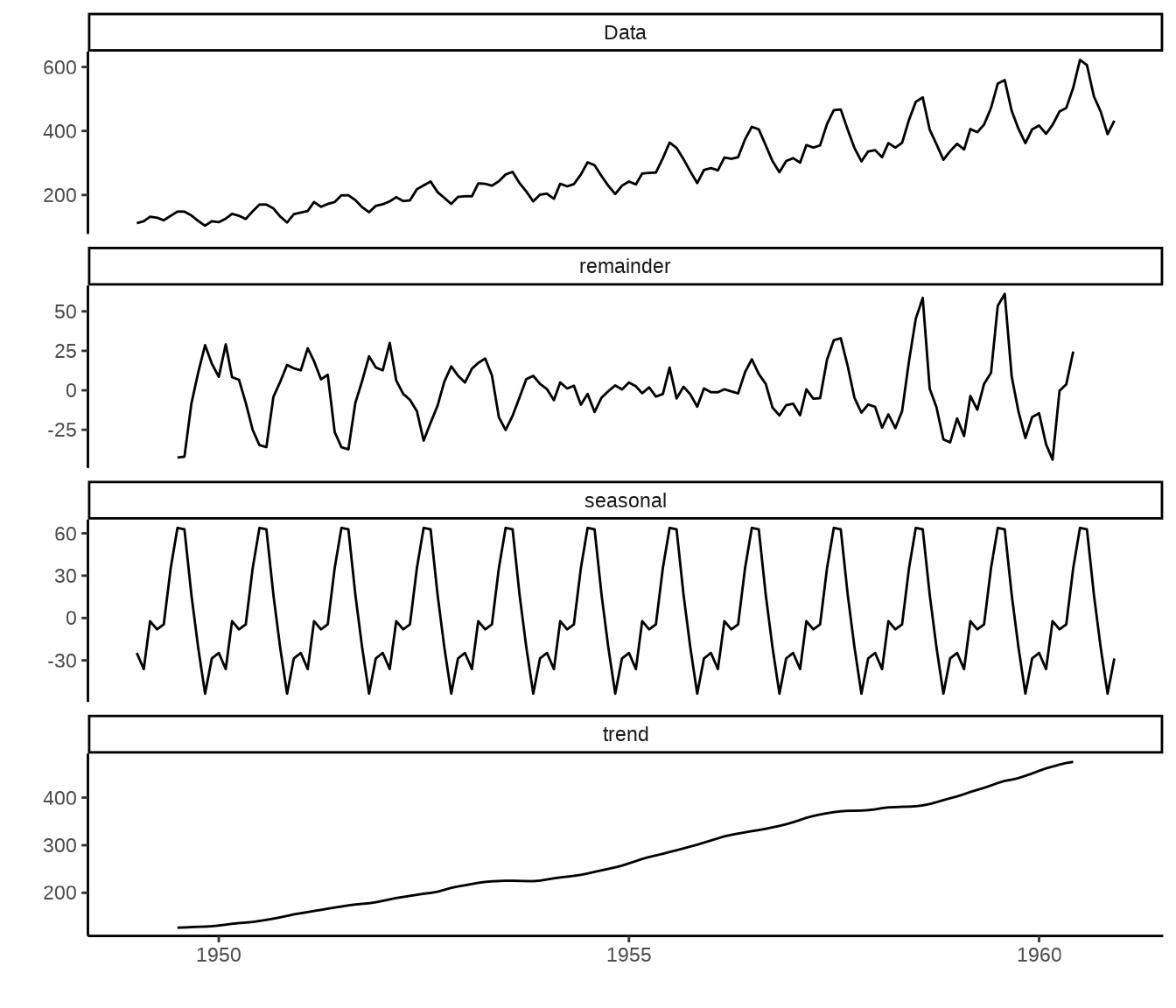
去掉季节性部分
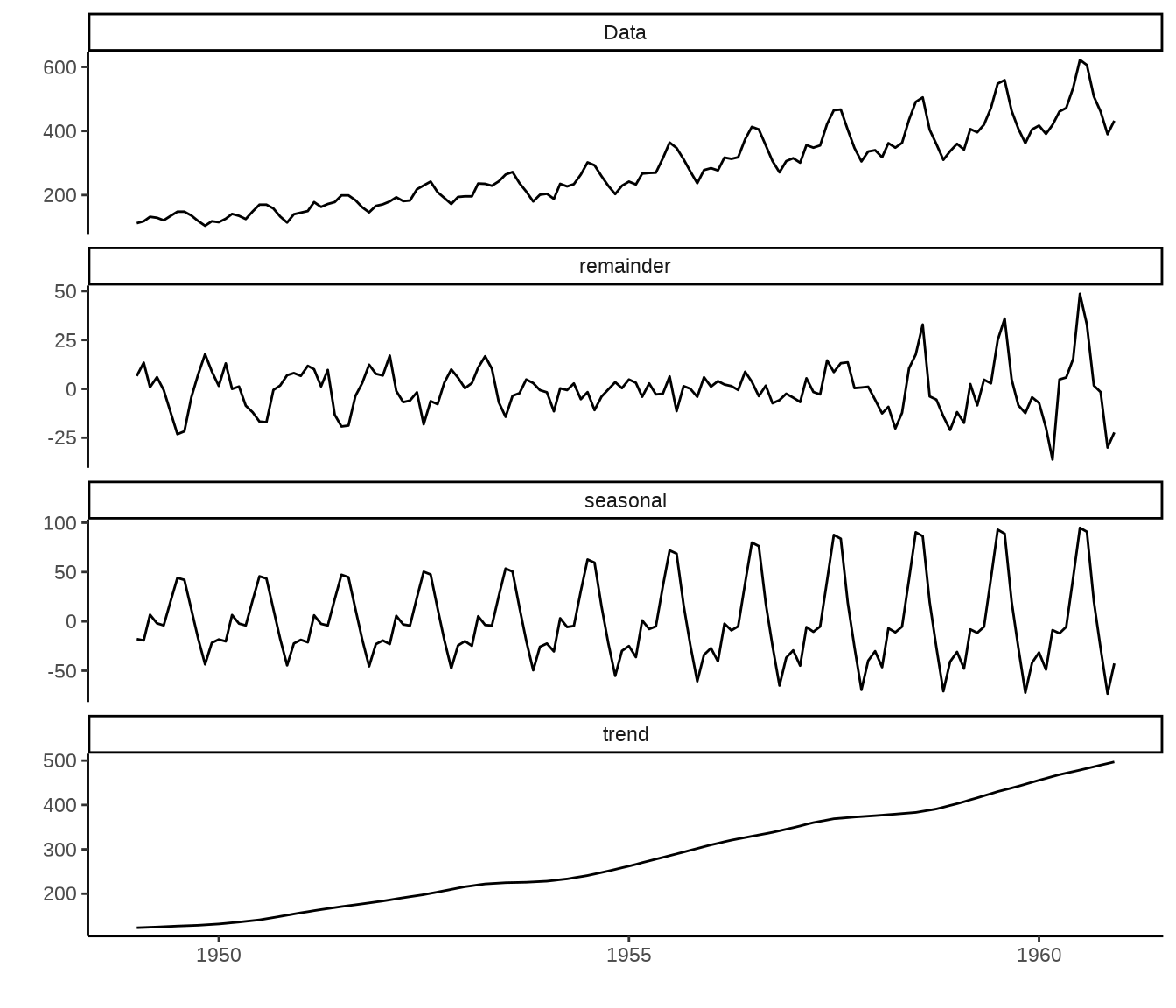
21.5.2 函数 stl()
函数 stl() 将时间序列分解为趋势性成分、季节性成分(周期性)、剩余成分。
剩余成分不是平稳序列,是异方差的。
xts 包的 periodicity() 函数可以检测时间序列数据的周期,但时序数据对象最好是在 xts 框架内。
21.6 经典时间序列模型
21.6.1 自回归模型
函数 ar() 拟合 AR 模型
21.6.2 移动平均模型
将自回归的阶设为 0,函数 arima() 也可以用来拟合 MA 模型。
21.6.3 自回归移动平均模型
函数 arima() 拟合 ARIMA 模型
Call:
arima(x = AirPassengers, order = c(1, 1, 3))
Coefficients:
ar1 ma1 ma2 ma3
0.5227 -0.2906 -0.3884 -0.1219
s.e. 0.1291 0.1284 0.1445 0.1322
sigma^2 estimated as 886: log likelihood = -688.45, aic = 1386.89forecast 包提供函数 auto.arima() 自动选择合适的自回归、差分和移动平均的阶来拟合数据。
Series: AirPassengers
ARIMA(2,1,1)(0,1,0)[12]
Coefficients:
ar1 ar2 ma1
0.5960 0.2143 -0.9819
s.e. 0.0888 0.0880 0.0292
sigma^2 = 132.3: log likelihood = -504.92
AIC=1017.85 AICc=1018.17 BIC=1029.3521.7 总结
方法没有好坏,只有适合与否。Holt-Winter 适合预警任务,算法简单,可以及时出预测结果,仅需要一步预测,不需要给出多步预测,要求快,以便迅速作出反应。Prophet 实现的贝叶斯结构可加模型适合短期预测任务,只要在可容许的时间范围内出结果即可,可以迅速出结果当然更好,需要给出多步预测结果,且结果需要强解释性,以便提前做一些商家供给、平台资源的分配。商分模型常常需要比较强的可解释性,算法策略模型重在预测精准度,对可解释性要求不高。
在时间序列数据的可视化方面,除了 Base R 提供的绘图方法外,静态的时序图 lattice 和 ggplot2 都不错,而交互式图形推荐使用 plotly 和 dygraphs。
PortfolioAnalytics 包做投资组合优化,均值-方差,收益和风险权衡。 Rmetrics 提供系列时间序列数据分析和建模的 R 包,包括投资组合优化 fPortfolio、多元分析 fMultivar、自回归条件异方差模型 fGarch、二元相依结构的 Copulae 分析 fCopulae 、市场和基础统计 fBasics 。
fable 一元到多元时间序列预测问题,提供 ETS、ARIMA、TSLM 等模型,并有书籍时间序列预测原则。值得一提, forecast 包开发者 Rob J Hyndman 称已不再开发新的功能,推荐大家使用 fable 包。feasts 包辅助特征抽取、序列分解、汇总统计和绘制图形等, 插件包 fable.prophet 接入 Prophet 的预测能力。timetk 时间序列数据处理、分析、预测和可视化工具箱,提供一致的操作方式,试图形成完成的解决方案。The Rmetrics Association 开发了一系列 R 包专门处理金融时间序列数据,比如 fGarch 包提供条件自回归异方差模型。
从时间序列中寻找规律,这样才是真的数据建模,从数据到模型,而不是相反 Finding Patterns in Time Series,识别金融时间序列的模式和统计规律。