21  优化问题

library(ROI)
library(ROI.plugin.glpk)
library(ROI.plugin.nloptr)
library(ROI.plugin.scs)
library(ROI.plugin.quadprog)
library(lattice)
# 自定义调色板
custom_palette <- function(irr, ref, height, saturation = 0.9) {
  hsv(
    h = height, s = 1 - saturation * (1 - (1 - ref)^0.5),
    v = irr
  )
}

21.1 旅行商问题

旅行商问题 The Traveling Salesman Problem 是一个混合整数线性规划问题，TSP 包 (Hahsler 和 Hornik 2007) 是求解此问题的最佳工具包。一般地，旅行商问题作如下定义。已知 \(n\) 个城市之间的距离，以矩阵 \(D\) 表示各个城市之间的距离，其元素 \(d_{ij}\) 表示城市 \(i\) 到城市 \(j\) 之间的距离，其对角元素 \(d_{ii} = 0\)，其中 \(i,j = 1,2,\cdots, n\) 。一个旅行路线可以用 \(\{1,2,\ldots,n\}\) 的循环排列 \(\pi\) 表示，\(\pi(i)\) 表示在旅行线路中跟在城市 \(i\) 之后的城市。旅行商问题就是找一个排列 \(\pi\) 使得如下旅行线路最短。

\[ \sum_{i=1}^{n} d_{i\pi(i)} \]

每个城市必须走到，且只能走一次。等价于如下整数规划问题，也是一个指派问题。

\[ \begin{aligned} \min ~ & \sum_{i=1}^{n}\sum_{j=1}^{n} d_{ij}x_{ij} \\ \text{s.t.} ~& \sum_{i=1}^{n}x_{ij} = 1, ~j = 1,2,\ldots,n, \\ ~& \sum_{j=1}^{n}x_{ij} = 1, ~ i = 1,2,\ldots,n, \\ ~& x_{ij} = 0 ~\text{or} ~ 1 \end{aligned} \]

某人要去美国 10 个城市旅行，分别是亚特兰大 Atlanta、芝加哥 Chicago、丹佛 Denver 、休斯顿 Houston、洛杉矶 Los Angeles、迈阿密 Miami、纽约 New York、旧金山 San Francisco、 西雅图 Seattle、华盛顿特区 Washington DC。10 个城市的分布如 图 21.1 所示。从洛杉矶出发，最后回到洛杉矶，如何规划旅行线路使得总行程最短？行程最短的路径是什么？

# 10 个城市的经纬度数据来自 maps 包的 us.cities 数据集
us_city_latlong <- read.table(file = textConnection("
City, Latitude, Longitude
Atlanta, 33.76, -84.42
Chicago, 41.84, -87.68
Denver, 39.77, -104.87
Houston, 29.77, -95.39
Los Angeles, 34.11, -118.41
Miami, 25.78, -80.21
New York, 40.67, -73.94
San Francisco, 37.77, -122.45
Seattle, 47.62, -122.35
Washington DC, 38.91, -77.01
"), header = TRUE, sep = ",")

library(sf)
us_city_latlong <- st_as_sf(us_city_latlong,
  coords = c("Longitude", "Latitude"), crs = 4326
)
library(ggplot2)
ggplot() +
  geom_sf_label(
    data = us_city_latlong, aes(label = City),
    fun.geometry = sf::st_centroid
  ) +
  geom_sf(data = us_city_latlong, color = "red") +
  coord_sf(crs = "ESRI:102003") +
  theme_bw() +
  labs(x = "经度", y = "纬度")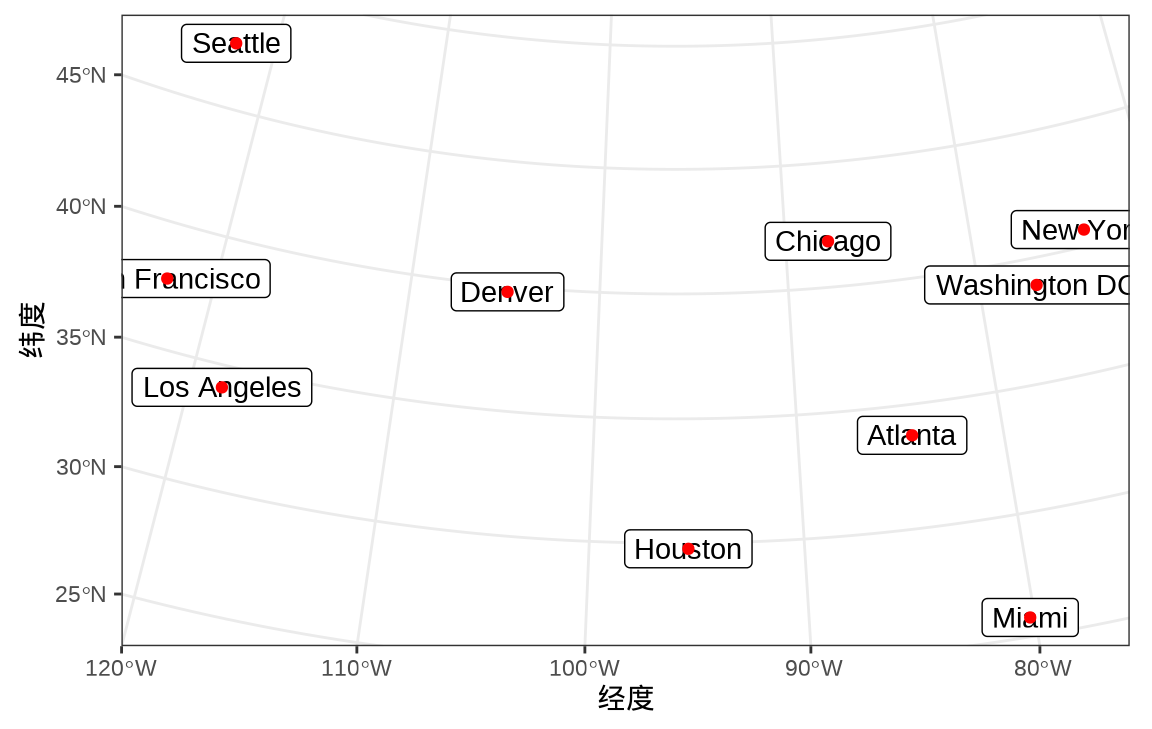

图 21.1: 10 个城市的分布图

简单起见，这 10 个城市之间的距离以直线距离代替，R 内置的数据集 UScitiesD 已经记录了这 10 个城市之间的直线距离。 UScitiesD 是一个 dist 类型的数据，可以用函数 as.matrix() 将其转化为矩阵类型。

data(UScitiesD)
D <- as.matrix(UScitiesD)
library(TSP)
D_tsp <- as.TSP(D)
# 出发城市洛杉矶
tour_sol <- solve_TSP(x = D_tsp, method = "nearest_insertion", start = 5)
tour_sol

#> object of class 'TOUR' 
#> result of method 'nearest_insertion' for 10 cities
#> tour length: 7373

途经 10 个城市的最短路程为 7373 。因采用启发式的随机优化算法，每次求解的结果可能会有所不同，建议运行多次，比较结果，选择最优的方法。

# 旅行最短路程
tour_length(tour_sol)

#> [1] 7373

# 旅行线路方案
as.integer(tour_sol)

#>  [1]  5  4  6  1 10  7  2  3  9  8

labels(D_tsp)[as.integer(tour_sol)]

#>  [1] "LosAngeles"    "Houston"       "Miami"         "Atlanta"      
#>  [5] "Washington.DC" "NewYork"       "Chicago"       "Denver"       
#>  [9] "Seattle"       "SanFrancisco"

求解结果对应的旅行方案，如 图 21.2 所示，依次走过的城市是：洛杉矶、旧金山、西雅图、丹佛、芝加哥、纽约、华盛顿特区、亚特兰大、迈阿密、休斯顿。

us_city_tour <- st_cast(st_combine(st_geometry(us_city_latlong[as.integer(tour_sol),])), "POLYGON")
ggplot() +
  geom_sf_label(
    data = us_city_latlong, aes(label = City),
    fun.geometry = sf::st_centroid
  ) +
  geom_sf(data = us_city_latlong, color = "red") +
  geom_sf(data = us_city_tour, fill = NA, color = "black") +
  coord_sf(crs = "ESRI:102003") +
  theme_bw() +
  labs(x = "经度", y = "纬度")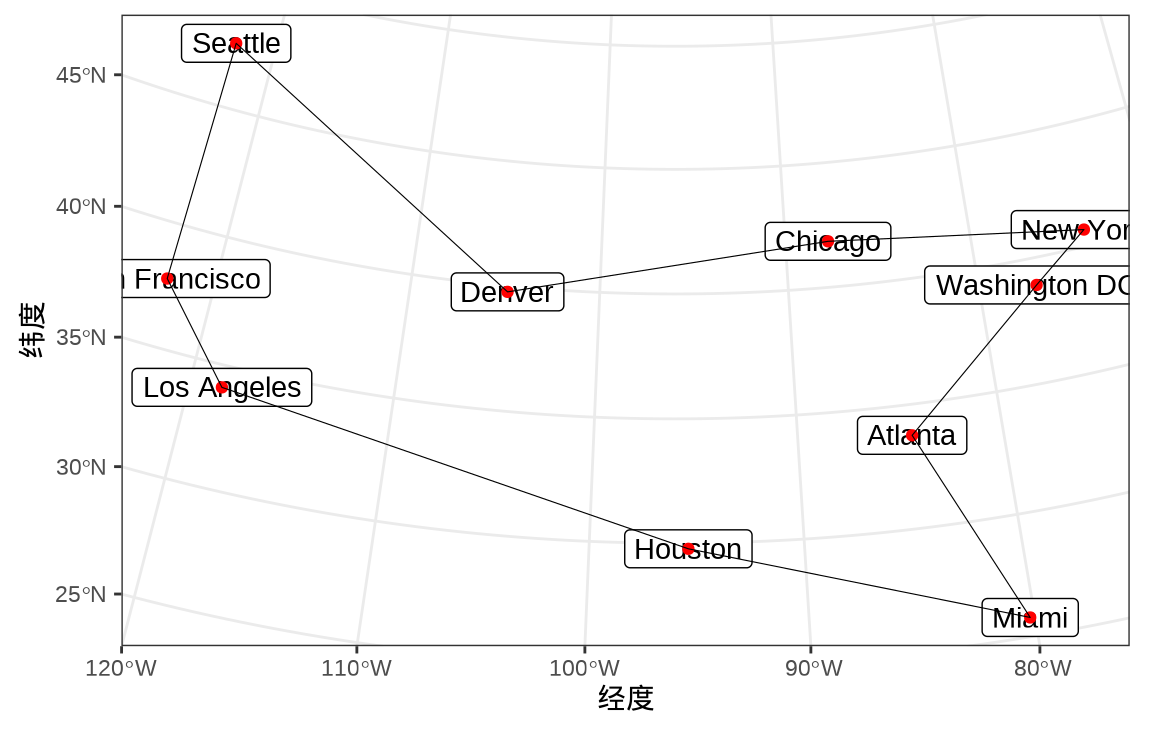

图 21.2: 10 个城市的路线图

21.2 投资组合问题

作为一个理性的投资者，希望回报最大而风险最小，给定投资和回报的约束条件下，选择风险最小的组合。一个简单的马科维茨投资组合优化问题如下：

\[ \begin{aligned} \min_{\boldsymbol{w}} \quad & \boldsymbol{w}^{\top}\hat{\Sigma}\boldsymbol{w} \\ \text{s.t.} \quad & A\boldsymbol{w}^{\top} \leq \boldsymbol{b} \end{aligned} \]

其中，\(\boldsymbol{w}\) 是权重向量，每个分量代表对投资对象的投资比例，\(\hat{\Sigma}\) 是关于投资对象的协方差矩阵，约束条件中包含两个部分，一个是权重之和为 1，一个是投资组合的收益率达到预期值。下面基于 12个科技公司公开的股价数据介绍此组合优化问题。

首先利用 quantmod 包获取微软、谷歌、亚马逊、惠普、甲骨文、英特尔、威瑞森、eBay、AT&T、Apple、Adobe 和 IBM 等 12 支股票的历史股价数据。根据 2022-11-01 至 2022-12-01 期间的股票调整价，计算各支股票天粒度的收益率。收益率可以看作一个随机变量，收益率的波动变化，即随机变量的方差，可以看作风险。

# 12 支股票的收益率
tech_stock_return <- readRDS(file = "data/tech_stock_return.rds")
DD <- 100 * tech_stock_return
# 平均收益率
r <- mean(DD)
r

#> [1] 0.3476413

# 目标函数
foo <- Q_objective(Q = cov(DD), L = rep(0, ncol(DD)))
# 投资约束
full_invest <- L_constraint(rep(1, ncol(DD)), "==", 1)
# 回报约束
target_return <- L_constraint(apply(DD, 2, mean), "==", r)
# 目标规划
op <- OP(objective = foo, constraints = rbind(full_invest, target_return))
op

#> ROI Optimization Problem:
#> 
#> Minimize a quadratic objective function of length 12 with
#> - 12 continuous objective variables,
#> 
#> subject to
#> - 2 constraints of type linear.
#> - 0 lower and 0 upper non-standard variable bounds.

求解器 nloptr.slsqp 需要给初值和等式约束的梯度，而求解器 quadprog 不需要给初值。下面使用 quadprog 来求解组合优化问题。

library(ROI.plugin.quadprog)
sol <- ROI_solve(op, solver = "quadprog")
# 最优解：投资组合
w <- sol$solution
# 保留 4 位小数
round(w, 4)

#>  [1] 0.0000 0.0000 0.0000 0.0000 0.3358 0.0000 0.0000 0.0000 0.3740 0.0000
#> [11] 0.0000 0.2902

# 目标函数值：投资风险
sqrt(t(w) %*% cov(DD) %*% w)

#>           [,1]
#> [1,] 0.9860861

求解出来的投资组合是甲骨文、 AT&T 和 IBM，投资比例分别是 33.58% 、37.40% 和 29.02% 。以上 12 支股票都属于科技公司，收益率具有非常高的相关性，因此，最终选出来 3 支。

与给定预期回报而风险最小的组合优化问题相对应的是另一个问题：给定风险的约束条件下，获得预期回报最大的组合。即求解如下组合优化问题：

\[ \begin{aligned} \max_{\boldsymbol{w}} \quad & \boldsymbol{w}^{\top}\hat{\boldsymbol{\mu}} \\ \text{s.t.} \quad & A\boldsymbol{w} \leq \boldsymbol{b} \\ \quad & \boldsymbol{w}^{\top}\hat{\Sigma}\boldsymbol{w} \leq \sigma \end{aligned} \]

其中，目标函数中 \(\hat{\boldsymbol{\mu}}\) 表示根据历史数据获得的投资对象的收益率，约束条件中 \(\sigma\) 表示投资者可以接受的投资风险，其他符号的含义同前。在给定风险约束 \(\sigma\) 下，求取回报最大的组合。线性约束也可以用函数 Q_constraint() 来表示，这样线性约束和二次约束可以整合在一起，代码如下：

# 风险阈值
sigma <- sqrt(t(w) %*% cov(DD) %*% w)
sigma

#>           [,1]
#> [1,] 0.9860861

# 12 阶的全 0 矩阵
zero_mat <- diag(x = rep(0, ncol(DD)))
# 目标函数
foo <- Q_objective(Q = zero_mat, L = colMeans(DD))
# 线性和二次约束
maxret_constr <- Q_constraint(
  Q = list(cov(DD), NULL),
  L = rbind(
    rep(0, ncol(DD)),
    rep(1, ncol(DD))
  ),
 dir = c("<=", "=="), rhs = c(1/2 * sigma^2, 1)
)
# 目标规划
op <- OP(objective = foo, constraints = maxret_constr, maximum = TRUE)
op

#> ROI Optimization Problem:
#> 
#> Maximize a quadratic objective function of length 12 with
#> - 12 continuous objective variables,
#> 
#> subject to
#> - 2 constraints of type quadratic.
#> - 0 lower and 0 upper non-standard variable bounds.

函数 ROI_applicable_solvers() 识别规划问题类型，给出可求解此规划问题的求解器。

ROI_applicable_solvers(op)

#> [1] "nloptr.cobyla" "nloptr.mma"    "nloptr.auglag" "nloptr.isres" 
#> [5] "nloptr.slsqp"

quadprog 求解器不能求解该问题，尝试求解器 nloptr.slsqp ，12 支股票同等看待，所以，权重的初始值都设置为 \(\frac{1}{12}\) 。

# 求解规划问题
nlp <- ROI_solve(op, solver = "nloptr.slsqp", start = rep(1/12, 12))
# 投资组合
w <- nlp$solution
# 保留 4 位小数
round(w, 4)

#>  [1] 0.0000 0.0000 0.0000 0.0000 0.3358 0.0000 0.0000 0.0000 0.3740 0.0000
#> [11] 0.0000 0.2902

# 投资组合的预期收益
w %*% colMeans(DD)

#>           [,1]
#> [1,] 0.3476413

结果显示，投资组合是甲骨文、 AT&T 和 IBM，投资比例分别是 33.58% 、37.40% 和 29.02% 。

值得注意，当约束条件比较复杂，比如包含一些非线性的等式或不等式约束，可以用函数 F_constraint() 来表示，这更加的灵活，但需要传递（非）线性约束的雅可比向量或矩阵。用函数 F_constraint() 表示的代码如下，求解结果是一样的。

# x 是一个表示权重的列向量 
# 等式约束
# 权重之和为 1 的约束
heq <- function(x) {
  sum(x)
}
# 等式约束的雅可比
heq.jac <- function(x) {
  rep(1, length(x))
}
# 不等式约束
# 二次的风险约束
hin <- function(x){
  1/2 * t(x) %*% cov(DD) %*% x
}
# 不等式约束的雅可比
hin.jac <- function(x){
  cov(DD) %*% x
}
# 目标规划
op <- OP(
  objective = L_objective(L = colMeans(DD)), # 12 个目标变量
  constraints = F_constraint(
    # 等式和不等式约束
    F = list(heq = heq, hin = hin),
    dir = c("==", "<="),
    rhs = c(1, 1/2 * sigma^2),
    # 等式和不等式约束的雅可比
    J = list(heq.jac = heq.jac, hin.jac = hin.jac)
  ),
  # 目标变量的取值范围
  bounds = V_bound(ld = 0, ud = 1, nobj = 12L),
  maximum = TRUE # 最大回报
)
op

#> ROI Optimization Problem:
#> 
#> Maximize a linear objective function of length 12 with
#> - 12 continuous objective variables,
#> 
#> subject to
#> - 2 constraints of type nonlinear.
#> - 0 lower and 12 upper non-standard variable bounds.

# 求解规划问题
nlp <- ROI_solve(op, solver = "nloptr.slsqp", start = rep(1/12, 12))
# 投资组合
w <- nlp$solution
round(w, 4)

#>  [1] 0.0000 0.0000 0.0000 0.0000 0.3358 0.0000 0.0000 0.0000 0.3740 0.0000
#> [11] 0.0000 0.2902

# 投资组合的预期收益
w %*% colMeans(DD)

#>           [,1]
#> [1,] 0.3476413

21.3 高斯过程回归

高斯过程回归模型如下：

\[ \boldsymbol{y}(x) = D\boldsymbol{\beta} + S(x) \]

其中，\(\boldsymbol{\beta}\) 是一个 \(p\times 1\) 维列向量，随机过程 \(S(x)\) 是均值为零，协方差为 \(V_{\boldsymbol{\theta}}\) 的平稳高斯过程，协方差矩阵 \(V_{\boldsymbol{\theta}}\) 的元素如下：

\[ \mathsf{Cov}\{S(x_i), S(x_j)\} = \sigma^2 \exp(-\|x_i - x_j\| / \phi) \]

其中， \(\boldsymbol{\theta} = (\sigma^2,\phi)\) 表示与协方差矩阵相关的参数，随机过程 \(S(x)\) 的一个实现服从多元正态分布 \(\mathrm{MVN}(\boldsymbol{0},V_{\boldsymbol{\theta}})\) ，则 \(\boldsymbol{y}(x)\) 也服从多元正态分布 \(\mathrm{MVN}(D\boldsymbol{\beta},V_{\boldsymbol{\theta}})\) 。参数 \(\boldsymbol{\beta}\) 的广义最小二乘估计为 \(\hat{\boldsymbol{\beta}}(\boldsymbol{\theta}) = (D^{\top}V_{\boldsymbol{\theta}}^{-1}D)^{-1} D^{\top}V_{\boldsymbol{\theta}}^{-1}\boldsymbol{y}\) ，关于参数 \(\boldsymbol{\theta}\) 的剖面对数似然函数如下：

\[ \log \mathcal{L}(\boldsymbol{\theta}) = -\frac{n}{2}\log (2\pi) - \frac{1}{2}\log (\det V_{\boldsymbol{\theta}}) -\frac{1}{2}\boldsymbol{y}^{\top}V_{\boldsymbol{\theta}}^{-1}\big(I - D(D^{\top}V_{\boldsymbol{\theta}}^{-1}D)^{-1}D^{\top}V_{\boldsymbol{\theta}}^{-1}\big)\boldsymbol{y} \]

下面考虑一个来自 MASS 包真实数据 topo。topo 数据集最初来自 John C. Davis （1973年）所著的书《Statistics and Data Analysis in Geology》。后来， J. J. Warnes 和 B. D. Ripley （1987年）以该数据集为例指出空间高斯过程的协方差函数的似然估计中存在的问题(Warnes 和 Ripley 1987)，并将其作为数据集 topo 放在 MASS 包里。Paulo J. Ribeiro Jr 和 Peter J. Diggle （2001年）将该数据集打包成自定义的 geodata 数据类型，放在 geoR 包里，并在他俩合著的书《Model-based Geostatistics》中多次出现。topo 是空间地形数据集，包含有 52 行 3 列，数据点是 310 平方英尺范围内的海拔高度数据，x 坐标每单位 50 英尺，y 坐标单位同 x 坐标，海拔高度 z 单位是英尺。

library(MASS)
data(topo)
str(topo)

#> 'data.frame':    52 obs. of  3 variables:
#>  $ x: num  0.3 1.4 2.4 3.6 5.7 1.6 2.9 3.4 3.4 4.8 ...
#>  $ y: num  6.1 6.2 6.1 6.2 6.2 5.2 5.1 5.3 5.7 5.6 ...
#>  $ z: int  870 793 755 690 800 800 730 728 710 780 ...

根据 topo 数据集， \(D = \boldsymbol{1}\) 是一个 \(52 \times 1\) 的列向量，\(\boldsymbol{\beta} = \beta\) 是一个截距项。设置参数初值 \((\sigma,\phi) = (65,2)\) 。为了与 Ripley 的论文中的图比较，下面扔掉了对数似然函数中常数项，用 R 语言编码的似然函数如下：

log_lik <- function(x) {
  n <- nrow(topo)
  D <- t(t(rep(1, n)))
  Sigma <- x[1]^2 * exp(-as.matrix(dist(topo[, c("x", "y")])) / x[2])
  inv_Sigma <- solve(Sigma)
  P <- diag(1, n) - D %*% solve(t(D) %*% solve(Sigma, D), t(D)) %*% inv_Sigma
  as.vector(-1 / 2 * log(det(Sigma)) - 1 / 2 * t(topo[, "z"]) %*% inv_Sigma %*% P %*% topo[, "z"])
}
log_lik(x = c(65, 2))

#> [1] -207.1364

关于参数的偏导计算复杂，就不计算梯度了，下面调用 R 软件内置的 nlminb 优化器。发现，对不同的初始值，收敛到不同的位置，目标函数值非常接近。

op <- OP(
  objective = F_objective(log_lik, n = 2L),
  bounds = V_bound(lb = c(55, 5), ub = c(75, 8)),
  maximum = TRUE
)
nlp <- ROI_solve(op, solver = "nlminb", start = c(65, 2))
nlp$solution

#> [1] 65  5

nlp$objval

#> [1] -197.4197

如果初始值靠近局部极值点，则就近收敛到该极值点，比如初值 \((65, 7)\) ， \((70, 7.5)\) 。

nlp <- ROI_solve(op, solver = "nlminb", start = c(65, 7))
nlp$solution

#> [1] 65  7

nlp$objval

#> [1] -196.9407

nlp <- ROI_solve(op, solver = "nlminb", start = c(70, 7.5))
nlp$solution

#> [1] 70.0  7.5

nlp$objval

#> [1] -196.8441

尝试调用来自 nloptr 包的全局优化求解器 nloptr.directL ，大大小小的坑都跳过去了，结果还是比较满意的。

nlp <- ROI_solve(op, solver = "nloptr.directL")
nlp$solution

#> [1] 63.934218  6.121339

nlp$objval

#> [1] -196.8158

目标区域网格化，计算格点处的似然函数值，然后绘制似然函数图像。

dat <- expand.grid(
  sigma = seq(from = 55, to = 75, length.out = 41),
  phi = seq(from = 5, to = 8, length.out = 31)
)
dat$fn <- apply(dat, 1, log_lik)

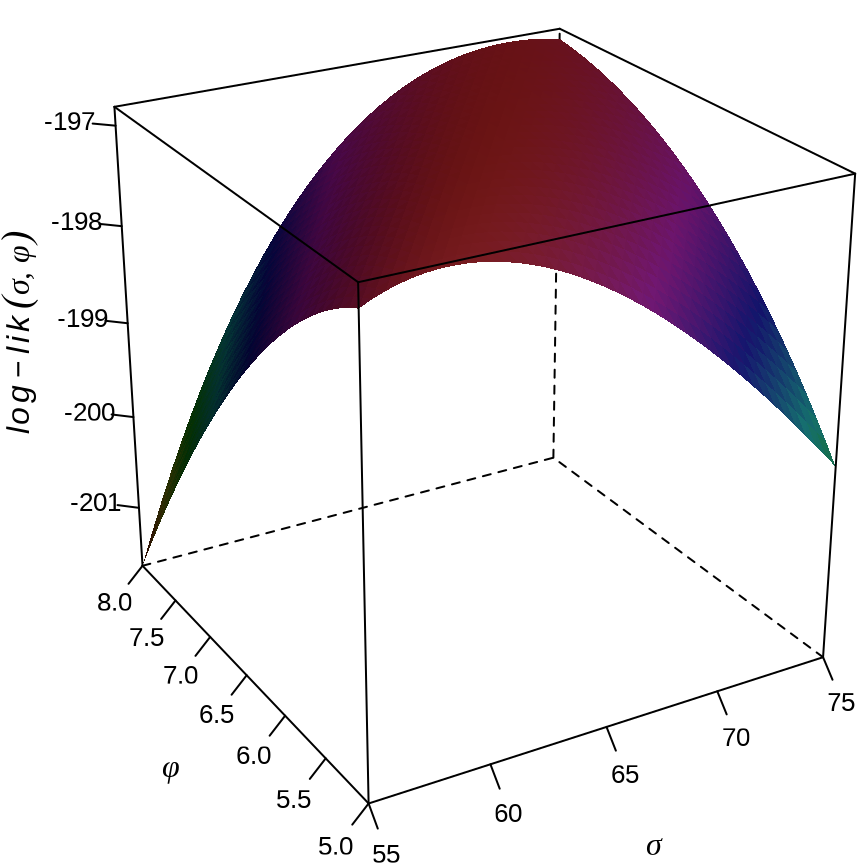
似然函数关于参数 \((\sigma,\phi)\) 的三维曲面见 图 21.3 。

wireframe(
  data = dat, fn ~ sigma * phi,
  shade = TRUE, drape = FALSE,
  xlab = expression(sigma), ylab = expression(phi),
  zlab = list(expression(
    italic(log-lik) ~ group("(", list(sigma, phi), ")")
  ), rot = 90),
  scales = list(arrows = FALSE, col = "black"),
  shade.colors.palette = custom_palette,
  # 减少三维图形的边空
  lattice.options = list(
    layout.widths = list(
      left.padding = list(x = -0.5, units = "inches"),
      right.padding = list(x = -1.0, units = "inches")
    ),
    layout.heights = list(
      bottom.padding = list(x = -1.5, units = "inches"),
      top.padding = list(x = -1.5, units = "inches")
    )
  ),
  par.settings = list(axis.line = list(col = "transparent")),
  screen = list(z = 30, x = -65, y = 0)
)

图 21.3: 对数似然函数的曲面图

等高线图呈现一道非常长且平滑的山岭 long flat ridge，山岭上布满许多局部极大值，普通的数值优化求解器常常陷入其中，只有全局优化求解器才可能找到全局极大值点。高斯过程回归模型的对数似然函数是非凸的，多模态的。

levelplot(fn ~ sigma * phi,
  data = dat, aspect = 1,
  xlim = c(54.5, 75.5), ylim = c(4.9, 8.1),
  xlab = expression(sigma), ylab = expression(phi),
  col.regions = cm.colors, contour = TRUE,
  scales = list(
    x = list(alternating = 1, tck = c(1, 0)),
    y = list(alternating = 1, tck = c(1, 0))
  ),
  # 减少三维图形的边空
  lattice.options = list(
    layout.widths = list(
      left.padding = list(x = 0, units = "inches"),
      right.padding = list(x = 0, units = "inches")
    ),
    layout.heights = list(
      bottom.padding = list(x = -.5, units = "inches"),
      top.padding = list(x = -.5, units = "inches")
    )
  )
)

图 21.4: 对数似然函数的等高线图

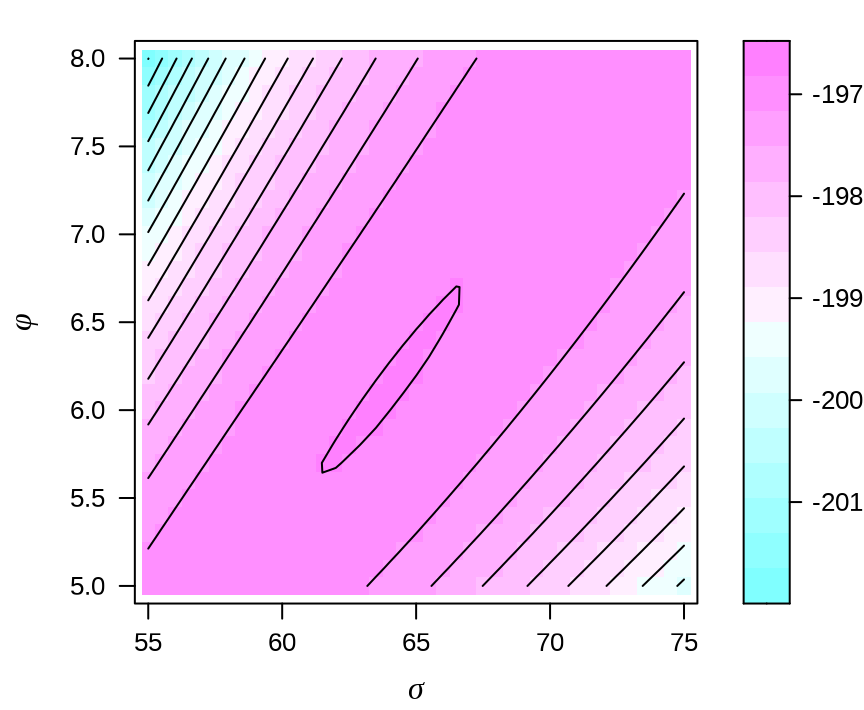
上图中没有看到许多局部极小值，与作者论文中的图 1 似乎不符。原因是什么？似然函数中涉及到的矩阵运算不精确，应该设计精度更高的运算方式？lattice 包绘图引擎无法展示更加细微的差异？还有一种解释，上图是对的，算法迭代时，对不同的初值，常常收敛到不同的结果，而这些不同的结果都位于岭上不同位置，对应的对数似然值却又几乎一样。

作为验证，下面调用 nlme 包的 gls() 函数拟合数据，参数的极大似然估计结果与全局优化求解器的结果比较一致。参数估计结果 \((\sigma, \phi)= (63.93429, 6.121352)\) ，对数似然函数值为 -244.6006 ，自编的似然函数 log_lik() 在最优解处的值为 -196.8158，再加上之前扔掉的常数项 -52 / 2 * log(2 * pi) ，就是 -244.6006 ，丝毫不差。

library(nlme)
fit_topo_ml <- gls(z ~ 1,
  data = topo, method = "ML",
  correlation = corExp(value = 65, form = ~ x + y)
)
summary(fit_topo_ml)

#> Generalized least squares fit by maximum likelihood
#>   Model: z ~ 1 
#>   Data: topo 
#>        AIC     BIC    logLik
#>   495.2012 501.055 -244.6006
#> 
#> Correlation Structure: Exponential spatial correlation
#>  Formula: ~x + y 
#>  Parameter estimate(s):
#>    range 
#> 6.121352 
#> 
#> Coefficients:
#>               Value Std.Error  t-value p-value
#> (Intercept) 863.708  45.49859 18.98318       0
#> 
#> Standardized residuals:
#>        Min         Q1        Med         Q3        Max 
#> -2.7169766 -1.1919732 -0.5272282  0.1453374  1.5061096 
#> 
#> Residual standard error: 63.93429 
#> Degrees of freedom: 52 total; 51 residual

如果使用限制极大似然估计，会发现参数估计结果与之相距甚远，而对数似然函数值相差无几。参数估计结果 \((\sigma,\phi) = (128.8275, 25.47324)\) 。

fit_topo_reml <- gls(z ~ 1,
  data = topo, method = "REML",
  correlation = corExp(value = 65, form = ~ x + y)
)
summary(fit_topo_reml)

#> Generalized least squares fit by REML
#>   Model: z ~ 1 
#>   Data: topo 
#>        AIC      BIC    logLik
#>   485.1558 490.9513 -239.5779
#> 
#> Correlation Structure: Exponential spatial correlation
#>  Formula: ~x + y 
#>  Parameter estimate(s):
#>    range 
#> 25.47324 
#> 
#> Coefficients:
#>                Value Std.Error  t-value p-value
#> (Intercept) 877.8956  116.7163 7.521619       0
#> 
#> Standardized residuals:
#>         Min          Q1         Med          Q3         Max 
#> -1.45850506 -0.70167923 -0.37178079 -0.03800119  0.63732032 
#> 
#> Residual standard error: 128.8275 
#> Degrees of freedom: 52 total; 51 residual

21.4 泊松混合分布

有限混合模型（Finite Mixtures of Distributions）的应用非常广泛，本节参考 BB 包 (Varadhan 和 Gilbert 2009) 的帮助手册，以泊松混合分布为例，介绍其参数的极大似然估计。更多详细的理论和算法介绍从略，感兴趣的读者可以查阅相关文献 (Hasselblad 1969)。BB 包比内置函数 optim() 功能更强，可以求解大规模非线性方程组，也可以求解带简单约束的非线性优化问题，还可以从多个初始值出发寻找全局最优解。

两个泊松分布以一定比例 \(p\) 混合，以概率 \(p\) 服从泊松分布 \(\mathrm{Poisson}(\lambda_1)\) ，而以概率 \(1-p\) 服从泊松分布 \(\mathrm{Poisson}(\lambda_1)\) 。

\[ p\times \mathrm{Poisson}(\lambda_1) + (1 - p)\times \mathrm{Poisson}(\lambda_2) \]

泊松混合分布的概率密度函数 \(f(x;p,\lambda_1,\lambda_2)\) 如下：

\[ f(x;p,\lambda_1,\lambda_2) = p \times \frac{\lambda_1^x \exp(-\lambda_1)}{x!} + (1 - p) \times \frac{\lambda_2^x \exp(-\lambda_2)}{x!} \]

随机变量 \(X\) 服从参数为 \(p\) 的伯努利分布 \(X \sim \mathrm{Bernoulli}(1, p)\) ，随机变量 \(Y\) 服从泊松混合分布，在伯努利分布的基础上，泊松混合分布也可作如下定义：

\[ \begin{array}{l} Y \sim \left\{ \begin{array}{l} \mathrm{Poisson}(\lambda_1), \quad \text{当} ~ X = 1 ~ \text{时},\\ \mathrm{Poisson}(\lambda_2), \quad \text{当} ~ X = 0 ~ \text{时}. \end{array} \right. \end{array} \]

对数似然函数如下：

\[ \ell(p,\lambda_1,\lambda_2) = \sum_{i=0}^{n}y_i \log\big(p\times \exp(-\lambda_1) \times\frac{\lambda_1^{x_i}}{x_i!} + (1 - p)\times \exp(-\lambda_2) \times\frac{\lambda_2 ^{x_i}}{x_i!} \big) \]

下 表格 21.1 数据来自 1947 年 Walter Schilling 发表在 JASA 的一篇文章 (Schilling 1947)。连续三年搜集伦敦《泰晤士报》刊登的死亡告示，每天的告示发布 80 岁及以上女性死亡人数。经过汇总统计，发现，在三年里，没有人死亡的告示出现 162 次，死亡 1 人的告示出现 267 次。

表格 21.1: 死亡人数的统计

死亡人数	0	1	2	3	4	5	6	7	8	9
发生频次	162	267	271	185	111	61	27	8	3	1

考虑到夏季和冬季对老人死亡率的影响是不同的，因此，引入泊松混合分布来对数据建模。

# 对数似然函数
# p 是一个长度为 3 的向量
# y 是观测数据向量
poissmix_loglik <- function(p, y) {
  i <- 0:(length(y) - 1)
  loglik <- y * log(p[1] * exp(-p[2]) * p[2]^i / exp(lgamma(i + 1)) +
    (1 - p[1]) * exp(-p[3]) * p[3]^i / exp(lgamma(i + 1)))
  sum(loglik)
}
# lgamma(i + 1) 表示整数 i 的阶乘的对数
# 参数的下限
lo <- c(0, 0, 0)
# 参数的上限
hi <- c(1, Inf, Inf)
# 随机生成一组参数初始值
p0 <- runif(3, c(0.2, 1, 1), c(0.8, 5, 8)) 
# 汇总统计出来的死亡人数的频次分布
y <- c(162, 267, 271, 185, 111, 61, 27, 8, 3, 1)

调用 BB 包的函数 BBoptim() 求解多元非线性箱式约束优化问题。

library(BB)
# 参数估计
ans <- BBoptim(
  par = p0, fn = poissmix_loglik, y = y,
  lower = lo, upper = hi, 
  control = list(maximize = TRUE)
)

#> iter:  0  f-value:  -2865.886  pgrad:  5.131972 
#> iter:  10  f-value:  -2001.398  pgrad:  0.01762828 
#>   Successful convergence.

ans

#> $par
#> [1] 0.7756704 2.0235472 2.6001739
#> 
#> $value
#> [1] -1998.702
#> 
#> $gradient
#> [1] 2.273737e-06
#> 
#> $fn.reduction
#> [1] -864.4886
#> 
#> $iter
#> [1] 12
#> 
#> $feval
#> [1] 104
#> 
#> $convergence
#> [1] 0
#> 
#> $message
#> [1] "Successful convergence"
#> 
#> $cpar
#> method      M 
#>      2     50

numDeriv::hessian 计算极大似然点的黑塞矩阵，然后计算参数估计的标准差。

# 黑塞矩阵
hess <- numDeriv::hessian(x = ans$par, func = poissmix_loglik, y = y)
hess

#>            [,1]       [,2]      [,3]
#> [1,] -201.15066  243.65862  46.62811
#> [2,]  243.65862 -277.80865 -97.47287
#> [3,]   46.62811  -97.47287 -20.57225

# 标准差
se <- sqrt(diag(solve(-hess)))

#> Warning in sqrt(diag(solve(-hess))): NaNs produced

se

#> [1] 0.10087468        NaN 0.09682762

multiStart 从不同初始值出发寻找全局最大值，先找一系列局部极大值，通过比较获得全局最大值。

# 随机生成 10 组初始值
p0 <- matrix(runif(30, c(0.2, 1, 1), c(0.8, 8, 8)), 
             nrow = 10, ncol = 3, byrow = TRUE)
ans <- multiStart(
  par = p0, fn = poissmix_loglik, action = "optimize",
  y = y, lower = lo, upper = hi, quiet = TRUE,
  control = list(maximize = TRUE, trace = FALSE)
)
# 筛选出迭代收敛的解
pmat <- round(cbind(ans$fvalue[ans$conv], ans$par[ans$conv, ]), 4)
dimnames(pmat) <- list(NULL, c("fvalue", "parameter 1", 
                               "parameter 2", "parameter 3"))
# 去掉结果一样的重复解
pmat[!duplicated(pmat), ]

#>         fvalue parameter 1 parameter 2 parameter 3
#> [1,] -1989.946      0.3599      1.2561      2.6634
#> [2,] -1989.946      0.6401      2.6634      1.2561
#> [3,] -1997.789      0.8482      2.0414      2.8545
#> [4,] -1999.421      0.9840      2.1014      6.1145

21.5 极大似然估计

一元函数最优化问题和求根问题是相关的。在统计应用中，二项分布的比例参数的置信区间估计涉及求根，伽马分布的参数的极大似然估计涉及求根。下面介绍求根在估计伽马分布的参数中的应用。

形状参数为 \(\alpha\) 和尺度参数为 \(\sigma\) 的伽马分布的概率密度函数 \(f(x;\alpha, \sigma)\) 如下：

\[ f(x;\alpha,\sigma) = \frac{1}{\sigma^\alpha \Gamma(\alpha)}x^{\alpha - 1} \exp(- \frac{x}{\sigma}), \quad \alpha \geq 0, \sigma > 0 \]

其中，\(\Gamma(\cdot)\) 表示伽马函数，伽马分布的均值为 \(\alpha \sigma\) ，方差为 \(\alpha\sigma^2\) 。下 图 21.5 展示两个伽马分布的概率密度函数，形状参数分别为 5 和 9，尺度参数均为 1，即伽马分布 \(f(x; 5, 1)\) 和 \(f(x; 9, 1)\) 。

ggplot() +
  geom_function(
    fun = dgamma, args = list(shape = 9, scale = 1),
    aes(colour = "list(alpha == 9, sigma == 1)"),
    linewidth = 1.2, xlim = c(0, 20), 
  ) +
  geom_function(
    fun = dgamma, args = list(shape = 5, scale = 1),
    aes(colour = "list(alpha == 5, sigma == 1)"),
    linewidth = 1.2, xlim = c(0, 20)
  ) +
  scale_colour_viridis_d(
    labels = scales::parse_format(),
    begin = 0.3, end = 0.7,
    option = "C"
  ) +
  theme_bw(base_family = "sans") +
  theme(axis.title = element_text(family = "Noto Serif CJK SC"),
        legend.title = element_text(family = "Noto Serif CJK SC"),
        legend.position = "top", legend.justification = "right") +
  labs(x = "随机变量", y = "概率密度", color = "参数")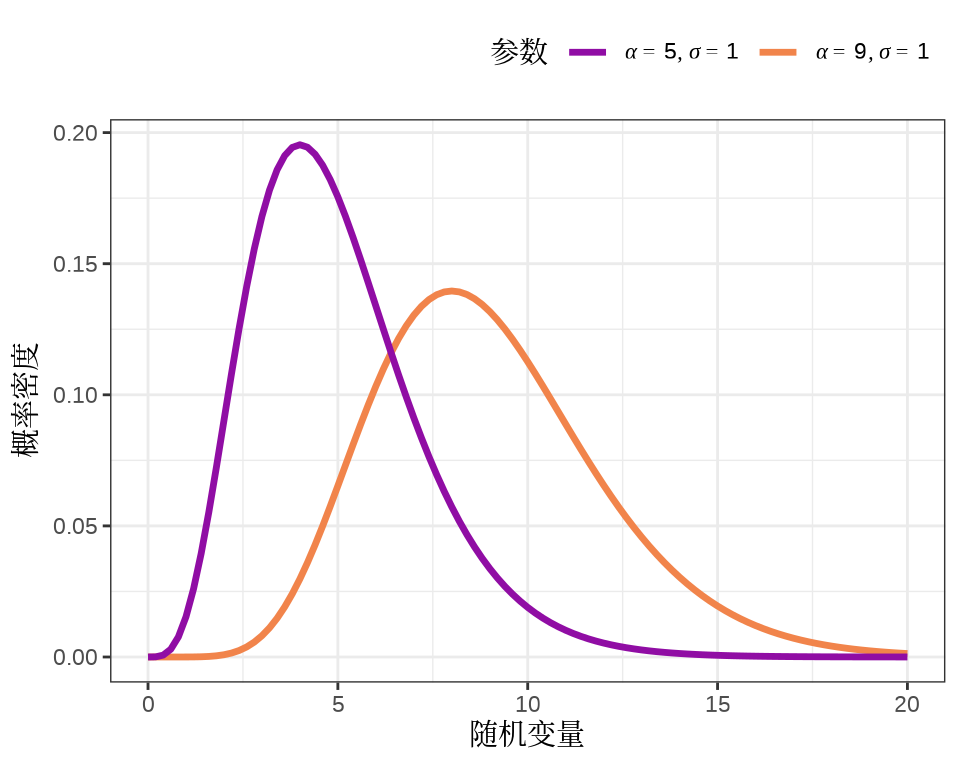

图 21.5: 伽马分布的概率密度函数

给定一组来自伽马分布的样本 \(x_1,x_2,\ldots,x_n\) ，关于参数 \(\alpha\) 和 \(\sigma\) 的似然函数如下：

\[ \mathcal{L}(\alpha, \sigma) = \big(\frac{1}{\sigma^\alpha \Gamma(\alpha)}\big)^{n} (\prod_{i=1}^{n} x_i)^{\alpha - 1} \exp(- \frac{ \sum_{i=1}^{n} x_i }{\sigma}) \]

则，其对数似然函数如下：

\[ \ell(\alpha, \sigma) = -n\big(\alpha \log(\sigma) + \log \Gamma(\alpha) \big) + (\alpha - 1)\sum_{i=1}^{n}\log(x_i) - \frac{ \sum_{i=1}^{n} x_i }{\sigma} \]

对数似然函数关于参数 \(\alpha\) 和 \(\sigma\) 的偏导数如下：

\[ \begin{aligned} \frac{\partial \ell(\alpha,\sigma)}{\partial \alpha} &= -n\Big( \log(\sigma) + \big(\log \Gamma(\alpha)\big)' \Big) + \sum_{i=1}^{n}\log (x_i) = 0 \\ \frac{\partial \ell(\alpha,\sigma)}{\partial \sigma} &= - \frac{n\alpha}{\sigma} + \frac{\sum_{i=1}^{n}x_i}{\sigma^2} = 0 \end{aligned} \]

根据第二个式子可得 \(\sigma = \frac{1}{n\alpha}\sum_{i=1}^{n}x_i\) ，将其代入第一个式子可得

\[ \log(\alpha) - \big(\log \Gamma(\alpha)\big)' = \log\big(\frac{1}{n}\sum_{i=1}^{n}x_i\big) - \frac{1}{n}\sum_{i=1}^{n}\log (x_i) \]

set.seed(20232023)
x <- rgamma(1000, shape = 1.5, scale = 2)
# 形状参数和尺度参数的矩估计
c(mean(x)^2 /var(x), var(x)/mean(x))

#> [1] 1.636030 1.902239

# 极大似然估计
# 常量
cc <- log(mean(x)) - mean(log(x))
# 方程
fun <- function(alpha){
  log(alpha) - digamma(alpha) - cc
}
# 找根
uniroot(f = fun, interval = c(1, 3))

#> $root
#> [1] 1.610272
#> 
#> $f.root
#> [1] 2.825244e-09
#> 
#> $iter
#> [1] 6
#> 
#> $init.it
#> [1] NA
#> 
#> $estim.prec
#> [1] 6.103516e-05

求得形状参数的估计 \(\alpha = 1.610272\) ，进而，可得尺度参数的估计 \(\sigma = 1.932667\) 。

函数 uniroot() 只能找到方程的一个根，rootSolve 包采用牛顿-拉弗森（ Newton-Raphson ）算法找一元非线性方程（组）的根，特别适合有多个根的情况。

library(rootSolve)
# 非线性方程（组）的根
multiroot(f = fun, start = 1.2)

#> $root
#> [1] 1.610272
#> 
#> $f.root
#> [1] 3.121097e-10
#> 
#> $iter
#> [1] 5
#> 
#> $estim.precis
#> [1] 3.121097e-10

# 搜索一个方程在区间内所有的根
uniroot.all(f = fun, interval = c(1, 3))

#> [1] 1.610339

21.6 习题

1. 某人要周游美国各州，从纽约出发，走遍 50 个州的行政中心，最后回到纽约。规划旅行线路使得总行程最短。Base R 内置的 R 包 datasets 包含美国 50 个州的地理中心数据 state.center 。

2. 有限混合模型也常用 EM 算法来估计参数，美国黄石公园老忠实间歇泉的喷发规律近似为二维高斯混合分布，请读者以 R 软件内置的数据集 faithful 为基础，采用 EM 算法估计参数。

3. 获取百度、阿里、腾讯、京东、美团、滴滴、字节、360、网易、新浪等 10 支股票的历史股价数据。根据 2021-12-01 至 2022-12-01 股票的调整价计算 12 个月的股价收益率，根据月度股价收益率和波动率数据，设置投资组合，使得月度收益率不低于2%。股票代码以数字编码和 HK 结尾的为港股代码，有的公司在美股和港股上都有。可以用 quantmod 包下载各个公司的股价数据，下载拼多多股价数据的代码如下：

   quantmod::getSymbols("PDD", auto.assign = FALSE, src = "yahoo")

   表格 21.2: 一些互联网公司及股票代码

   公司	美团	阿里巴巴	京东	百度	腾讯	拼多多	京东	阿里巴巴
   股票代码	3690.HK	9988.HK	9618.HK	9888.HK	0700.HK	PDD	JD	BABA

Hahsler, Michael, 和 Kurt Hornik. 2007. 《TSP: Infrastructure for the traveling salesperson problem》. Journal of Statistical Software 23 (2): 1–21. https://doi.org/10.18637/jss.v023.i02.

Hasselblad, Victor. 1969. 《Estimation of Finite Mixtures of Distributions from the Exponential Family》. Journal of the American Statistical Association 64 (328): 1459–71. https://doi.org/10.1080/01621459.1969.10501071.

Schilling, Walter. 1947. 《A Frequency Distribution Represented as the Sum of Two Poisson Distributions》. Journal of the American Statistical Association 42 (239): 407–24.

Varadhan, Ravi, 和 Paul Gilbert. 2009. 《BB: An R Package for Solving a Large System of Nonlinear Equations and for Optimizing a High-Dimensional Nonlinear Objective Function》. Journal of Statistical Software 32 (4): 1–26. https://www.jstatsoft.org/v32/i04/.

Warnes, J. J., 和 B. D. Ripley. 1987. 《Problems with likelihood estimation of covariance functions of spatial gaussian processes》. Biometrika 74 (3): 640–42.