13 常见的统计分布

三大抽样分布 t 分布，\(\chi^2\) 分布和 F 分布，一元和多元情形，一元分布知识范围是本科，多元分布范围是研究生和博士。一元分布多用于本科假设检验，多元分布常用于均值向量和协方差阵以及统计量的极限分布。

library(mvtnorm)
library(MASS)
library(lattice)

13.1 正态分布

公式：期望、方差
图像：密度分布、累积分布
模拟：随机数、分位点、积分、期望、方差

13.1.1 一元情形

x = rnorm(1000, mean = 0, sd = 1)
mean(x)

#> [1] 0.03118218

sd(x)

#> [1] 1.008863

plot(x, col = densCols(x, colramp = terrain.colors),
     pch = 20, panel.first = grid(), cex = 1)

13.1.2 多元情形

多元正态分布函数 (MVN)

\[ \Phi(\mathbf{a},\mathbf{b},\Sigma)=\frac{1}{\sqrt{|\Sigma|(2\pi)^m}} \int_{a_1}^{b_1}\!\int_{a_2}^{b_2}\!\cdots\!\int_{a_m}^{b_m} e^{-\frac{1}{2}x^\top\Sigma^{-1}x}dx \]

其中 \(x = (x_1,x_2,\dots,x_m)^\top, \forall i, -\infty \le a_i \le b_i \le \infty\)， \(\Sigma\) 是 \(m \times m\) 对称非负定的矩阵

下面使用 MASS 包的 mvrnorm() 函数模拟一组抽取自多元正态分布的样本。

library(MASS)
n <- 1000 # 样本量
X <- mvrnorm(n,
  mu = rep(0, 2),
  Sigma = matrix(c(1, 0.8, 0.8, 1),
    ncol = 2, byrow = TRUE
  )
)

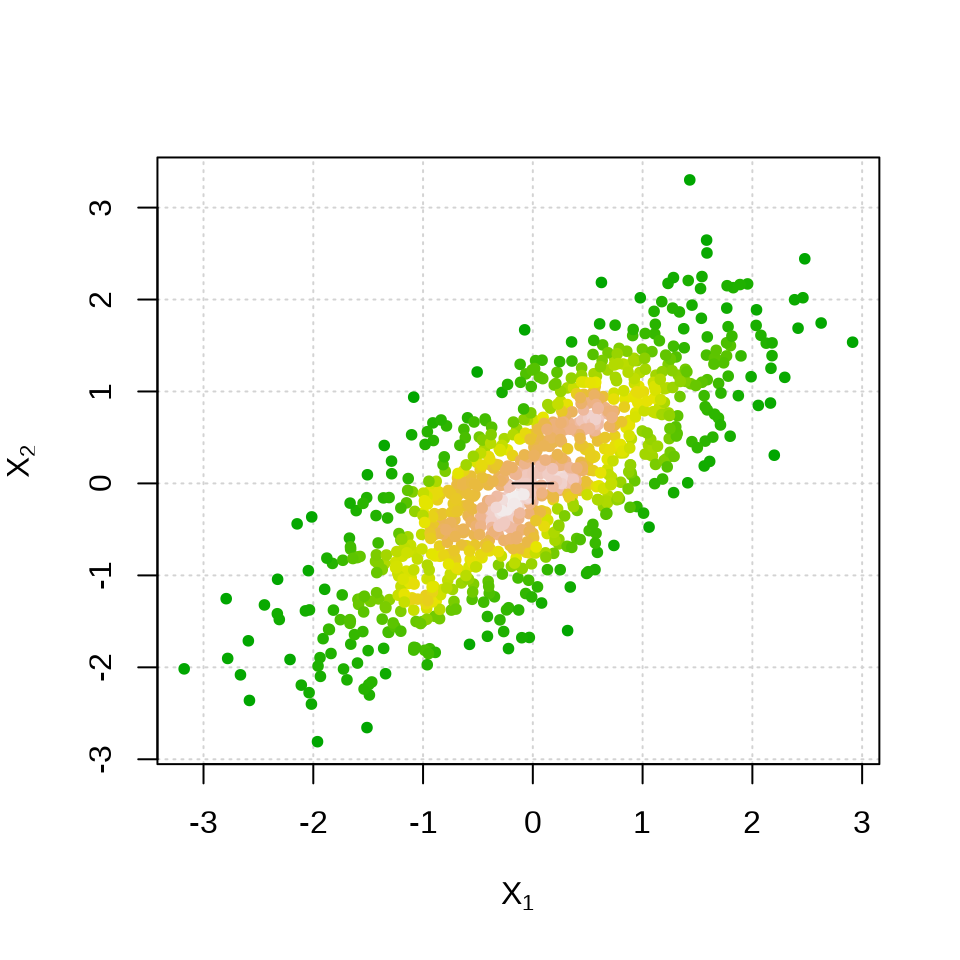
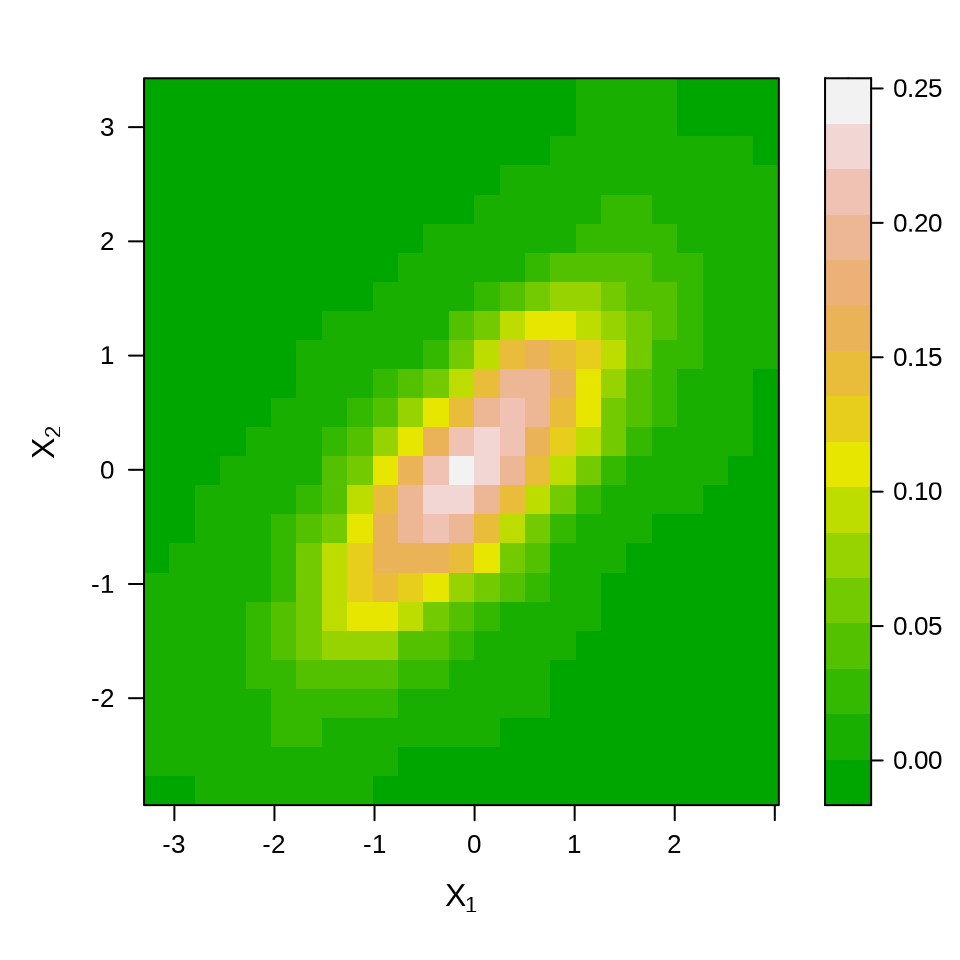
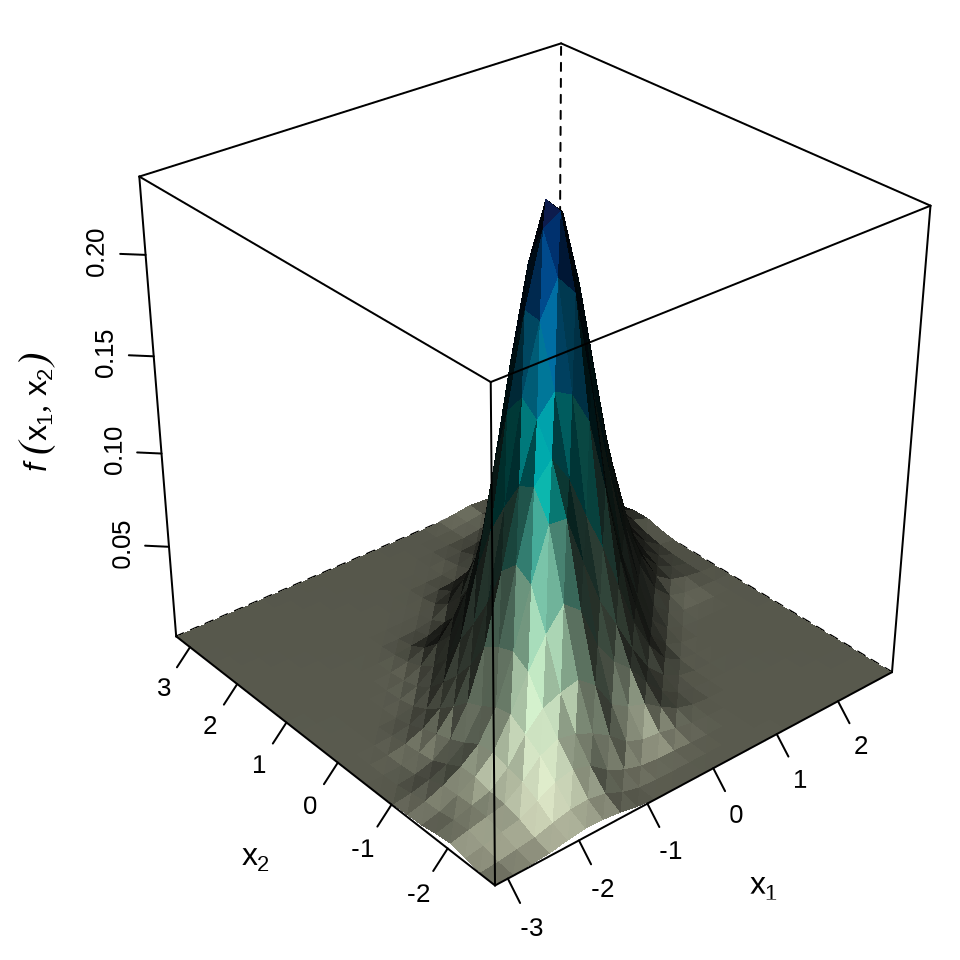
二维正态分布的图像见下图，分别是散点图、栅格图和三维透视图

代码

# 散点图
plot(X,
  pch = 20, panel.first = grid(), cex = 1,
  col = densCols(X, colramp = terrain.colors),
  xlab = expression(X[1]), ylab = expression(X[2])
)
points(x = 0, y = 0, pch = 3, cex = 2)
# 栅格图
f1 <- kde2d(X[, 1], X[, 2], n = 25)
df <- data.frame(expand.grid(x = f1$x, y = f1$y), z = as.vector(f1$z))
library(lattice)
levelplot(
  z ~ x * y,
  data = df, 
  col.regions = terrain.colors,
  xlab = expression(X[1]), 
  ylab = expression(X[2]), 
  scales = list(
    draw = TRUE, # 坐标轴刻度
    # 去掉图形上边、右边多余的刻度线
    x = list(alternating = 1, tck = c(1, 0)),
    y = list(alternating = 1, tck = c(1, 0))
  )
)
# 透视图
wireframe(
  data = df, z ~ x * y, shade = TRUE, drape = FALSE,
  xlab = expression(x[1]), ylab = expression(x[2]),
  zlab = list(expression(italic(f) ~ group("(", list(x[1], x[2]), ")")), rot = 90),
  scales = list(arrows = FALSE, col = "black", z = list(rot = 90)),
  # 减少三维图形的边空
  lattice.options = list(
    layout.widths = list(
      left.padding = list(x = -0.5, units = "inches"),
      right.padding = list(x = -1.0, units = "inches")
    ),
    layout.heights = list(
      bottom.padding = list(x = -1.5, units = "inches"),
      top.padding = list(x = -1.5, units = "inches")
    )
  ),
  par.settings = list(
    axis.line = list(col = "transparent")
  )
)

mvtnorm 包的函数 pmvnorm() 计算多元正态分布的概率，这个例子来自链接

library(mvtnorm)
# 模拟一个协方差矩阵
sigma <- matrix(c(1, 0.8, 0.8, 1), nrow = 2)
m <- nrow(sigma)
Fn <- pmvnorm(
  lower = rep(-Inf, m), upper = rep(0, m),
  mean = rep(0, m), sigma = sigma
)
Fn

#> [1] 0.3975836
#> attr(,"error")
#> [1] 1e-15
#> attr(,"msg")
#> [1] "Normal Completion"

13.2 t 分布

13.2.1 一元情形

13.2.2 多元情形

多元 t 分布函数 (MVT)

\[ T(\mathbf{a},\mathbf{b},\Sigma,\nu)=\frac{2^{1-\frac{\nu}{2}}}{\Gamma(\frac{\nu}{2}) } \int_{0}^{\infty} s^{\nu-1}e^{-\frac{s^2}{2}} \Phi(\frac{s\mathbf{a}}{\sqrt{\nu}},\frac{s\mathbf{b}}{\sqrt{\nu}},\Sigma)ds \]

多元 \(t\) 分布分位数计算

library(mvtnorm)
n <- c(26, 24, 20, 33, 32)
V <- diag(1 / n)
df <- 130
C <- matrix(c(
  1, 1, 1, 0, 0, -1, 0, 0, 1, 0,
  0, -1, 0, 0, 1, 0, 0, 0, -1, -1,
  0, 0, -1, 0, 0
), ncol = 5)
cv <- C %*% V %*% t(C) ## covariance matrix
dv <- t(1 / sqrt(diag(cv)))
cr <- cv * (t(dv) %*% dv) ## correlation matrix
delta <- rep(0, 5)
Tn <- qmvt(0.95,
  df = df, delta = delta, corr = cr,
  abseps = 0.0001, maxpts = 100000, tail = "both"
)
Tn

#> $quantile
#> [1] 2.561114
#> 
#> $f.quantile
#> [1] 2.606519e-07
#> 
#> attr(,"message")
#> [1] "Normal Completion"

13.3 F 分布

F 分布 R. A. Fisher

13.3.1 一元情形

13.3.2 多元情形

13.4 卡方分布

卡方分布 \(\chi^2\) Karl Person

13.4.1 一元情形

13.4.2 多元情形

13.5 威沙特分布

Wishart 分布

Theodore W. Anderson 的博士论文研究非中心的 Wishart 分布，以 Wishart（威沙特）分布的构造过程串一串统计分布的情况，比如和 \(\chi^2\) 分布的关系。Wishart 分布的表示和构造借助 Cholesky 分解

13.6 霍特林分布

霍特林分布 \(T^2\)