14  分类数据的分析

\[ \def\bm#1{{\boldsymbol #1}} \]

1. 最常见的两个广义线性模型：泊松和逻辑回归
2. 理论公式、R 输出及其解释，应用案例
3. 与计数/离散数据的假设检验的关系
4. 辛普森悖论，分类数据处理，高维列联表的压缩和分层，边际和条件
5. 泰坦尼克号 4x2x2x2 高维复杂列联表分析

library(MASS)

计数数据，通俗来说，对象是一个一个或一份一份的，可数的、离散的数据，比如人数。列联表来组织数据，分二维和多维的情况。

14.1 比例检验

14.1.1 单样本检验

比例检验函数 prop.test() 检验比例是否等于给定的值。单样本的比例检验结果中比例的区间估计与 Wilson 区间估计 (Wilson 1927) 是相关的。区间估计与假设检验是有紧密关系的，对于二项分布比例的 11 种区间估计方法的比较 (Newcombe 1998)。

14.1.1.1 近似检验

14.1.1.2 精确检验

函数 binom.test() 来做二项检验，函数 binom.test() 用来检验伯努利试验中成功概率 \(p\) 和给定概率 \(p_0\) 的关系，属于精确检验 (Clopper 和 Pearson 1934)。

比例 \(p\) 的检验，做 \(n\) 次独立试验，样本 \(X_1,\ldots,X_n \sim b(1, p)\)，事件发生的总次数 \(\sum_{i=1}^{n}X_i\)。

# 模拟一组样本
set.seed(20232023)
x <- sample(x = c(0, 1), size = 100, replace = TRUE, prob = c(0.8, 0.2))

二项分布中成功概率的检验

binom.test(sum(x), n = 100, p = 0.5)

#> 
#>  Exact binomial test
#> 
#> data:  sum(x) and 100
#> number of successes = 23, number of trials = 100, p-value = 5.514e-08
#> alternative hypothesis: true probability of success is not equal to 0.5
#> 95 percent confidence interval:
#>  0.1517316 0.3248587
#> sample estimates:
#> probability of success 
#>                   0.23

检验成功概率 p 是否等于 0.5， P 值 \(5.514 \times 10^{-8}\) 结论是拒绝原假设

binom.test(sum(x), n = 100, p = 0.2)

#> 
#>  Exact binomial test
#> 
#> data:  sum(x) and 100
#> number of successes = 23, number of trials = 100, p-value = 0.4534
#> alternative hypothesis: true probability of success is not equal to 0.2
#> 95 percent confidence interval:
#>  0.1517316 0.3248587
#> sample estimates:
#> probability of success 
#>                   0.23

检验成功概率 p 是否等于 0.2， P 值 0.4534 结论是不能拒绝原假设

切比雪夫不等式（Chebyshev, 1821-1894）。设随机变量 \(X\) 的数学期望和方差都存在，则对任意常数 \(\epsilon > 0\)，有

\[ \begin{aligned} P(|X - EX| \geq \epsilon) & \leq \frac{Var(X)}{\epsilon^2} \\ P(|X - EX| \leq \epsilon) & \geq 1 - \frac{Var(X)}{\epsilon^2} \end{aligned} \]

14.1.2 两样本检验

关于两样本的比例检验问题

\[ \begin{aligned} H_0: P_A = P_B \quad vs. \quad H_1: P_A > P_B \\ H_0: P_A = P_B \quad vs. \quad H_1: P_A < P_B \end{aligned} \]

\(H_0\) 成立的情况下，暗示着两个样本来自同一总体。

比例检验函数 prop.test() 用来检验两组或多组二项分布的成功概率（比例）是否相等。

设随机变量 X 服从参数为 \(p\) 的二项分布 \(b(n, p)\)， \(Y\) 服从参数为 \(\theta\) 的二项分布 \(b(m,\theta)\)， \(m,n\) 都假定为较大的正整数，检验如下问题

\[ H_0: P_A \geq P_B \quad vs. \quad H_1: P_A < P_B \]

根据中心极限定理

\[ \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{p(1-p)}{n} + \frac{\theta(1-\theta)}{m}}} \]

近似服从标准正态分布 \(N(0,1)\)。如果用矩估计 \(\bar{X}\) 和 \(\bar{Y}\) 分别替代总体参数 \(p\) 和 \(\theta\)，构造检验统计量

\[ T = \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{\bar{X}(1-\bar{X})}{n} + \frac{\bar{Y}(1-\bar{Y})}{m}}} \]

根据 Slutsky 定理，检验统计量 \(T\) 近似服从标准正态分布，当 \(T\) 偏大时，拒绝 \(H_0\)。该方法的优势在于当 \(n,m\) 比较大时，二项分布比较复杂，无法建立统计表，利用标准正态分布表来给出检验所需要的临界值，简便易行！

当 \(p\) 和 \(\theta\) 都比较小，上述方法检验效果不好，原因在于由中心极限定理对 \(\bar{X}\) 和 \(\bar{Y}\) 的正态分布近似效果不好，或者间接地导致 \(\bar{X}-\bar{Y}\) 的方差偏小，进而 \(T\) 的分辨都不好，而且当 \(p,\theta\) 很接近 1 时，上述现象也会产生！

下面介绍新的解决办法，办法来自两个二项总体成功概率的比较 (宋泽熙 2011)。

上面的检验问题等价于

\[ H_0: \frac{P_A}{P_B} \geq 1 \quad vs. \quad H_1: \frac{P_A}{P_B} < 1 \]

引入检验统计量

\[ T^{\star} = \frac{\bar{X}}{\bar{Y}} \]

同样由 Slutsky 定理和中心极限定理可知， \(\bar{X}/\bar{Y}\) 近似服从 正态分布 \(\mathcal{N}(1,\frac{1-\theta}{m\theta})\)

当 \((T^\star - 1)/\hat\sigma\) 偏大时接受 \(H_0\)，临界值可通过 \(\mathcal{N}(0, \hat\sigma^2)\) 分布表计算得到， \(\hat\sigma^2\) 是对 \(\frac{1-\theta}{m\theta}\) 的估计，比如取 \(\hat\sigma^2 = \frac{1-\bar{Y}}{m}\cdot \frac{1}{\bar{Y}}\) 或取 \(\hat\sigma^2 = \frac{1-\bar{Y}}{m}\cdot \frac{1}{\bar{X}}\)

由于渐近方差形如 \(\frac{1-\theta}{m\theta}\)，因而在 \(\theta\) 较小，渐近方差较大，克服了之前 \(\bar{X} - \bar{Y}\)的方差较小的问题

\(p,\theta\) 很接近 1 时，我们取检验统计量

\[ T^{\star\star} = \frac{1-\bar{Y}}{1-\bar{X}} \]

结论和 \(T^\star\) 类似，当 \(T^{\star\star}\) 偏大时，拒绝 \(H_0\)。

14.1.3 多样本检验

14.1.3.1 比例齐性检验

对多组数据的比例检验，可以理解为比例齐性检验。

14.1.3.2 比例趋势检验

比例趋势检验函数 prop.trend.test() 的原假设：四个组里面病人中吸烟的比例是相同的。备择假设：四个组的吸烟比例是有趋势的。

\[ \begin{aligned} & H_0: P_1 = P_2 = P_3 = P_4 \\ & H_1: P_1 < P_2 < P_3 < P_4 ~\text{或者}~ P_1 > P_2 > P_3 > P_4 \end{aligned} \]

smokers <- c(83, 90, 129, 70)
patients <- c(86, 93, 136, 82)
prop.test(smokers, patients)

#> 
#>  4-sample test for equality of proportions without continuity correction
#> 
#> data:  smokers out of patients
#> X-squared = 12.6, df = 3, p-value = 0.005585
#> alternative hypothesis: two.sided
#> sample estimates:
#>    prop 1    prop 2    prop 3    prop 4 
#> 0.9651163 0.9677419 0.9485294 0.8536585

prop.trend.test(smokers, patients)

#> 
#>  Chi-squared Test for Trend in Proportions
#> 
#> data:  smokers out of patients ,
#>  using scores: 1 2 3 4
#> X-squared = 8.2249, df = 1, p-value = 0.004132

14.2 泊松检验

泊松分布是 1837年由法国数学家泊松 （Poisson, 1781-1840） 首次提出。

\[ p(x) = \frac{\lambda^x\exp(-\lambda)}{x!}, x = 0, 1, \cdots . \]

泊松分布的期望和方差都是 \(\lambda\) ，一般要求 \(\lambda > 0\)。

14.2.1 单样本

poisson.test() 泊松分布的参数 \(\lambda\) 的精确检验，适用于单样本和两样本。

poisson.test(x,
  T = 1, r = 1,
  alternative = c("two.sided", "less", "greater"),
  conf.level = 0.95
)

参数 T 数据的时间单位

14.2.2 两样本

14.3 列联表描述

泰坦尼克号乘客生存死亡统计数据，Titanic 数据集

Titanic

#> , , Age = Child, Survived = No
#> 
#>       Sex
#> Class  Male Female
#>   1st     0      0
#>   2nd     0      0
#>   3rd    35     17
#>   Crew    0      0
#> 
#> , , Age = Adult, Survived = No
#> 
#>       Sex
#> Class  Male Female
#>   1st   118      4
#>   2nd   154     13
#>   3rd   387     89
#>   Crew  670      3
#> 
#> , , Age = Child, Survived = Yes
#> 
#>       Sex
#> Class  Male Female
#>   1st     5      1
#>   2nd    11     13
#>   3rd    13     14
#>   Crew    0      0
#> 
#> , , Age = Adult, Survived = Yes
#> 
#>       Sex
#> Class  Male Female
#>   1st    57    140
#>   2nd    14     80
#>   3rd    75     76
#>   Crew  192     20

14.3.1 行列分组表格

# 长格式转宽格式
titanic_data <- reshape(
  data = as.data.frame(Titanic), direction = "wide",
  idvar = c("Class", "Sex", "Age"),
  timevar = "Survived", v.names = "Freq", sep = "_"
)

# 制作表格
gt::gt(titanic_data) |> 
  gt::cols_label(
    Freq_Yes = "存活",
    Freq_No = "死亡",
    Class = "船舱",
    Sex = "性别",
    Age = "年龄"
  )

表格 14.1: 泰坦尼克号乘客生存死亡统计数据

船舱	性别	年龄	死亡	存活
1st	Male	Child	0	5
2nd	Male	Child	0	11
3rd	Male	Child	35	13
Crew	Male	Child	0	0
1st	Female	Child	0	1
2nd	Female	Child	0	13
3rd	Female	Child	17	14
Crew	Female	Child	0	0
1st	Male	Adult	118	57
2nd	Male	Adult	154	14
3rd	Male	Adult	387	75
Crew	Male	Adult	670	192
1st	Female	Adult	4	140
2nd	Female	Adult	13	80
3rd	Female	Adult	89	76
Crew	Female	Adult	3	20

14.3.2 百分比堆积图

泰坦尼克号处女航乘客数量按船舱、性别、年龄和存活情况分层， ggstats 包绘制百分比堆积柱形图展示多维分类数据。

library(ggplot2)
library(ggstats)
ggplot(as.data.frame(Titanic)) +
  aes(x = Class, fill = Survived, weight = Freq, by = Class) +
  geom_bar(position = "fill") +
  scale_y_continuous(labels = scales::label_percent()) +
  geom_text(stat = "prop", position = position_fill(.5)) +
  facet_grid(~Sex) +
  labs(x = "船舱", y = "比例", fill = "存活")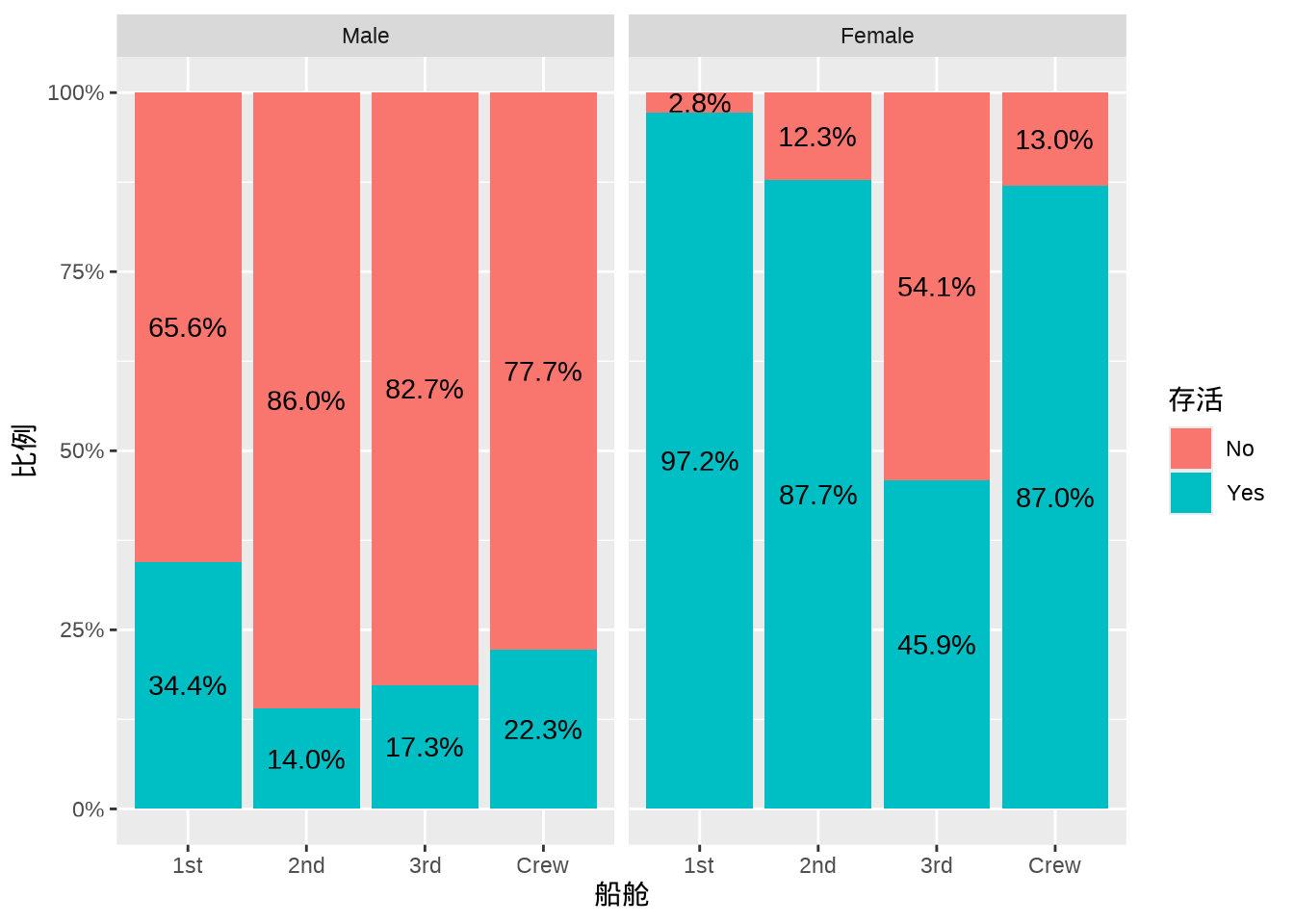

图 14.1: 百分比堆积柱形图展示多维分类数据

ggstats 包提供的图层 stat_prop() 是 stat_count() 的变种， as.data.frame(Titanic) 中 Age 一列会自动聚合吗？ by = Class 按 Class 分组聚合，统计 Survived 的比例，提供 prop 计算的变量，传递给 geom_text() 以添加注释，position 设置将注释放在柱子的中间

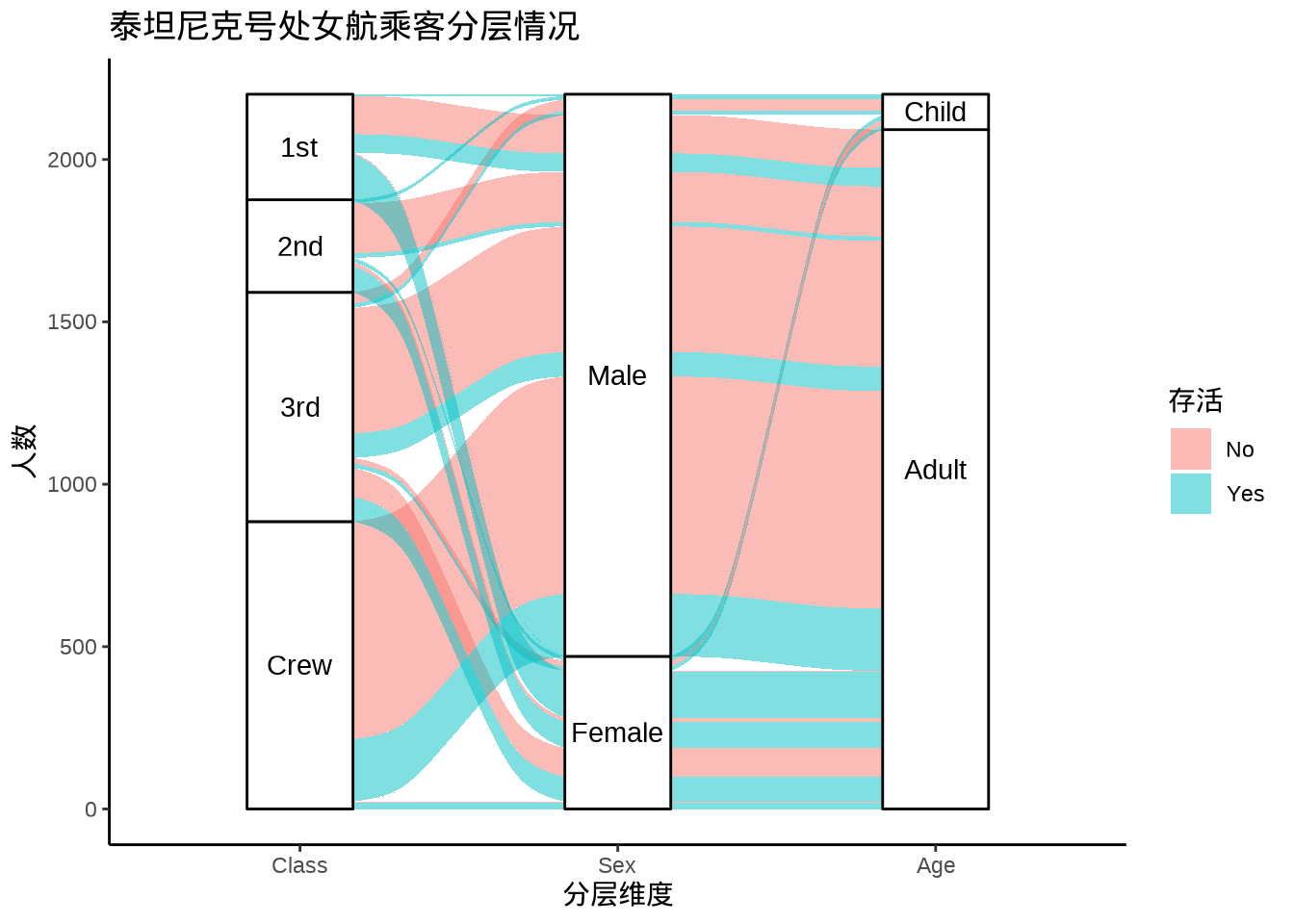
14.3.3 桑基图

用 ggalluvial 包(Brunson 2020)绘制桑基图展示多维分类数据。

library(ggplot2)
library(ggalluvial)
ggplot(
  data = as.data.frame(Titanic),
  aes(axis1 = Class, axis2 = Sex, axis3 = Age, y = Freq)
) +
  scale_x_discrete(limits = c("Class", "Sex", "Age")) +
  geom_alluvium(aes(fill = Survived)) +
  geom_stratum() +
  geom_text(stat = "stratum", aes(label = after_stat(stratum))) +
  theme_classic() +
  labs(
    x = "分层维度", y = "人数", fill = "存活",
    title = "泰坦尼克号处女航乘客分层情况"
  )

图 14.2: 桑基图展示多维分类数据

14.3.4 马赛克图

op <- par(mar = c(2.5, 2.5, 1.5, 0.5))
mosaicplot(~ Class + Sex + Age + Survived,
  data = Titanic, # shade = TRUE, 
  color = TRUE, border = "white",
  xlab = "船舱", ylab = "性别", main = "泰坦尼克号")
par(op)

图 14.3: 马赛克图展示多维分类数据

vcd 包针对分类数据做了很多专门的可视化工作，内置了很多数据集和绘图函数，在 Base R 绘图基础上，整合了许多统计分析功能，提供了一个统一的可视化框架(Meyer, Zeileis, 和 Hornik 2006; Zeileis, Meyer, 和 Hornik 2007)，更多细节见著作《Discrete Data Analysis with R: Visualization and Modeling Techniques for Categorical and Count Data》及其附带的 R 包 vcdExtra(Friendly 和 Meyer 2016)。

library(grid)
library(vcd)
mosaic(~ Class + Sex + Age + Survived,
  data = Titanic, shade = TRUE, legend = TRUE
)

图 14.4: 马赛克图展示多维分类数据

14.4 列联表分析

是否应该按照列联表的维度分类？还是应该从分析的目的和作用出发？比如我的目的是检验独立性。二者似乎也并不冲突。

列联表中的数据服从多项分布，关于独立性检验，有如下几种常见类型：

1. 相互独立 Mutual independence 所有变量之间相互独立，\(X \perp Y \perp Z\) 。
2. 联合独立 Joint independence 两个变量的联合与第三个变量独立，\(XY \perp Z\) 。
3. 边际独立 Marginal independence 当忽略第三个变量时，两个变量是独立的。列联表压缩
4. 条件独立 Conditional independence 当固定第三个变量时，两个变量是独立的，\(X \perp Y | Z\)。

本节数据来自著作《An Introduction to Categorical Data Analysis》(Agresti 2007) 的第2章习题 2.33，探索 1976-1977 年美国佛罗里达州的凶杀案件中被告肤色和死刑判决的关系。

tbl <- expand.grid(
  Death = c("Yes", "No"), # 判决结果 是否死刑
  Defend = c("白人", "黑人"),  # 被告 肤色
  Victim = c("白人", "黑人")   # 原告 （被害人）肤色
)
ethnicity <- data.frame(tbl, Freq = c(19, 132, 11, 52, 0, 9,  6, 97))

# 长格式转宽格式
dat1 <- reshape(
  data = ethnicity, direction = "wide",
  idvar = c("Defend", "Victim"),
  timevar = "Death", v.names = "Freq", sep = "_"
)
# 制作表格
gt::gt(dat1) |> 
  gt::cols_label(
    Freq_Yes = "是",
    Freq_No = "否",
    Victim = "被害人",
    Defend = "被告"
  ) |> 
  gt::tab_spanner(
    label = "死刑",
    columns = c(Freq_Yes, Freq_No)
  ) |> 
  gt::opt_row_striping()

表格 14.2: 佛罗里达州的凶杀案件统计数据

被告	被害人	死刑
		是	否
白人	白人	19	132
黑人	白人	11	52
白人	黑人	0	9
黑人	黑人	6	97

14.4.1 相互独立性

皮尔逊卡方检验（ Pearson’s \(\chi^2\) 检验） chisq.test() 常用于列联表独立性检验和方差分析模型的拟合优度检验。下面是一个 \(2 \times 2\) 的列联表。

卡方独立性检验

	第一列	第二列	合计
第一行	\(a\)	\(b\)	\(a+b\)
第二行	\(c\)	\(d\)	\(c+d\)
合计	\(a+c\)	\(b+d\)	\(a+b+c+d\)

# Death 死刑与 Defend （被告）独立性检验
m <- xtabs(Freq ~ Death + Defend, data = ethnicity)
m

#>      Defend
#> Death 白人 黑人
#>   Yes   19   17
#>   No   141  149

chisq.test(m, correct = TRUE)

#> 
#>  Pearson's Chi-squared test with Yates' continuity correction
#> 
#> data:  m
#> X-squared = 0.086343, df = 1, p-value = 0.7689

chisq.test(m, correct = FALSE)

#> 
#>  Pearson's Chi-squared test
#> 
#> data:  m
#> X-squared = 0.22145, df = 1, p-value = 0.6379

当被告是白人时，死刑判决 19 个，占总的死刑判决数量的 19/36 = 52.78%，当被告是黑人时，死刑判决 17 个，占总的死刑判决数量的 17/36 = 47.22%。判决结果与被告种族没有显著关系，但与原告（受害人）种族是有关系的，请继续往下看。

# Death 死刑与 Victim （原告）独立性检验
m <- xtabs(Freq ~ Death + Victim, data = ethnicity)
chisq.test(m, correct = TRUE)

#> 
#>  Pearson's Chi-squared test with Yates' continuity correction
#> 
#> data:  m
#> X-squared = 4.7678, df = 1, p-value = 0.029

chisq.test(m, correct = FALSE)

#> 
#>  Pearson's Chi-squared test
#> 
#> data:  m
#> X-squared = 5.6149, df = 1, p-value = 0.01781

当受害人是白人时，死刑判决 30 个，占总的死刑判决数量的 30/36 = 83.33%，当受害人是黑人时，死刑判决 6 个，占总的死刑判决数量的 6/36 = 16.67%。受害人是白人时，死刑判决明显多于黑人。

多维列联表

m <- xtabs(Freq ~ Death + Defend + Victim, data = ethnicity)
m

#> , , Victim = 白人
#> 
#>      Defend
#> Death 白人 黑人
#>   Yes   19   11
#>   No   132   52
#> 
#> , , Victim = 黑人
#> 
#>      Defend
#> Death 白人 黑人
#>   Yes    0    6
#>   No     9   97

判决结果、被告种族、原告种族三者是否存在联合独立性，即考虑 (Victim, Death) 是否与 Defend 独立，(Victim, Defend) 是否与 Death 独立，(Death, Defend) 与 Victim 是否相互独立。

fm <- loglin(table = m, margin = list(c(1, 2), c(1, 3), c(2, 3)), print = FALSE)
fm 

#> $lrt
#> [1] 0.7007504
#> 
#> $pearson
#> [1] 0.3751739
#> 
#> $df
#> [1] 1
#> 
#> $margin
#> $margin[[1]]
#> [1] "Death"  "Defend"
#> 
#> $margin[[2]]
#> [1] "Death"  "Victim"
#> 
#> $margin[[3]]
#> [1] "Defend" "Victim"

# 拟合对数线性模型
# fm <- loglin(m, list(c(1), c(2), c(3)))
# fm

似然比检验统计量（Likelihood Ratio Test statistic），皮尔逊 \(\chi^2\) 统计量（Pearson X-square Test statistic）

1 - pchisq(fm$lrt, fm$df)

#> [1] 0.4025317

拟合对数线性模型

fit_dvp <- glm(Freq ~ ., data = ethnicity, family = poisson(link = "log"))

模型输出

summary(fit_dvp)

#> 
#> Call:
#> glm(formula = Freq ~ ., family = poisson(link = "log"), data = ethnicity)
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)  2.45087    0.18046  13.582  < 2e-16 ***
#> DeathNo      2.08636    0.17671  11.807  < 2e-16 ***
#> Defend黑人   0.03681    0.11079   0.332     0.74    
#> Victim黑人  -0.64748    0.11662  -5.552 2.83e-08 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for poisson family taken to be 1)
#> 
#>     Null deviance: 395.92  on 7  degrees of freedom
#> Residual deviance: 137.93  on 4  degrees of freedom
#> AIC: 181.61
#> 
#> Number of Fisher Scoring iterations: 5

Pearson \(\chi^2\) 统计量

sum(residuals(fit_dvp, type = "pearson")^2)

#> [1] 122.3975

MASS 包计算模型参数的置信区间

confint(fit_dvp, trace = FALSE)

#>                  2.5 %     97.5 %
#> (Intercept)  2.0802598  2.7893934
#> DeathNo      1.7546021  2.4493677
#> Defend黑人  -0.1803969  0.2543149
#> Victim黑人  -0.8790491 -0.4213701

对于单元格总样本量小于 40 或 T 小于 1 时，需采用费希尔精确检验（ Fisher ’s Exact 检验）。

14.4.2 边际独立性

费希尔精确检验：固定边际的情况下，检验列联表行和列之间的独立性 fisher.test() 。

fisher.test() 函数用法，统计原理和公式，适用范围和条件，概念背景和历史。

费舍尔 (Sir Ronald Fisher, 1890.2 – 1962.7)¹ 和一位女士打赌，女士说能品出奶茶中奶和茶的添加顺序。

fisher.test() 针对计数数据，检验列联表中行和列的独立性。

TeaTasting <- matrix(c(3, 1, 1, 3),
  nrow = 2,
  dimnames = list(
    Guess = c("Milk", "Tea"),
    Truth = c("Milk", "Tea")
  )
)
TeaTasting

#>       Truth
#> Guess  Milk Tea
#>   Milk    3   1
#>   Tea     1   3

# 单边 P 值
fisher.test(TeaTasting, alternative = "greater")

#> 
#>  Fisher's Exact Test for Count Data
#> 
#> data:  TeaTasting
#> p-value = 0.2429
#> alternative hypothesis: true odds ratio is greater than 1
#> 95 percent confidence interval:
#>  0.3135693       Inf
#> sample estimates:
#> odds ratio 
#>   6.408309

# 双边 P 值
fisher.test(TeaTasting, alternative = "two.sided")

#> 
#>  Fisher's Exact Test for Count Data
#> 
#> data:  TeaTasting
#> p-value = 0.4857
#> alternative hypothesis: true odds ratio is not equal to 1
#> 95 percent confidence interval:
#>    0.2117329 621.9337505
#> sample estimates:
#> odds ratio 
#>   6.408309

# 单边 P 值
sum(dhyper(x = c(3, 4), m = 4, n = 4, k = 4))

#> [1] 0.2428571

14.4.3 对称性

用于计数数据的 McNemar 卡方检验（ McNemar \(\chi^2\) 检验）：检验二维列联表行和列的对称性 mcnemar.test()。怎么理解对称性？其实是配对检验。看帮助实例。

Performance <- matrix(c(794, 86, 150, 570),
  nrow = 2,
  dimnames = list(
    "1st Survey" = c("Approve", "Disapprove"),
    "2nd Survey" = c("Approve", "Disapprove")
  )
)
Performance

#>             2nd Survey
#> 1st Survey   Approve Disapprove
#>   Approve        794        150
#>   Disapprove      86        570

mcnemar.test(Performance)

#> 
#>  McNemar's Chi-squared test with continuity correction
#> 
#> data:  Performance
#> McNemar's chi-squared = 16.818, df = 1, p-value = 4.115e-05

14.4.4 条件独立性

用于分层分类数据的 Cochran-Mantel-Haenszel 卡方检验：两个枚举（分类）变量的条件独立性，假定不存在三个因素的交互作用。Cochran-Mantel-Haenszel 检验 mantelhaen.test()

str(UCBAdmissions)

#>  'table' num [1:2, 1:2, 1:6] 512 313 89 19 353 207 17 8 120 205 ...
#>  - attr(*, "dimnames")=List of 3
#>   ..$ Admit : chr [1:2] "Admitted" "Rejected"
#>   ..$ Gender: chr [1:2] "Male" "Female"
#>   ..$ Dept  : chr [1:6] "A" "B" "C" "D" ...

UCBAdmissions 数据集是一个 \(2\times 2 \times 6\) 的三维列联表，R 语言中常用 table 类型表示。实际上，table 类型衍生自 array 数组类型，当把 UCBAdmissions 当作一个数组操作时，1、2、3 分别表示 Admit、Gender、Dept 三个维度。

mantelhaen.test(UCBAdmissions)

#> 
#>  Mantel-Haenszel chi-squared test with continuity correction
#> 
#> data:  UCBAdmissions
#> Mantel-Haenszel X-squared = 1.4269, df = 1, p-value = 0.2323
#> alternative hypothesis: true common odds ratio is not equal to 1
#> 95 percent confidence interval:
#>  0.7719074 1.0603298
#> sample estimates:
#> common odds ratio 
#>         0.9046968

没有证据表明院系与性别之间存在关联。在给定院系的情况下，是否录取和性别没有显著关系。

# 按系统计
apply(UCBAdmissions, 3, function(x) (x[1, 1] * x[2, 2]) / (x[1, 2] * x[2, 1]))

#>         A         B         C         D         E         F 
#> 0.3492120 0.8025007 1.1330596 0.9212838 1.2216312 0.8278727

woolf <- function(x) {
  x <- x + 1 / 2
  k <- dim(x)[3]
  or <- apply(x, 3, function(x) (x[1, 1] * x[2, 2]) / (x[1, 2] * x[2, 1]))
  w <- apply(x, 3, function(x) 1 / sum(1 / x))
  1 - pchisq(sum(w * (log(or) - weighted.mean(log(or), w))^2), k - 1)
}
woolf(UCBAdmissions)

#> [1] 0.0034272

14.5 加州伯克利分校的录取情况

1973 年加州伯克利分校 6 个最大的院系的录取情况见下 表格 14.3 ，研究目标是加州伯克利分校在招生录取工作中是否有性别歧视？

表格 14.3: 加州伯克利分校的录取情况

院系	录取		拒绝
	男性	女性	男性	女性
A	512	89	313	19
B	353	17	207	8
C	120	202	205	391
D	138	131	279	244
E	53	94	138	299
F	22	24	351	317

借助马赛克图 图 14.5 可以更加直观的看出数据中的比例关系。

图 14.5: 加州伯克利分校院系录取情况

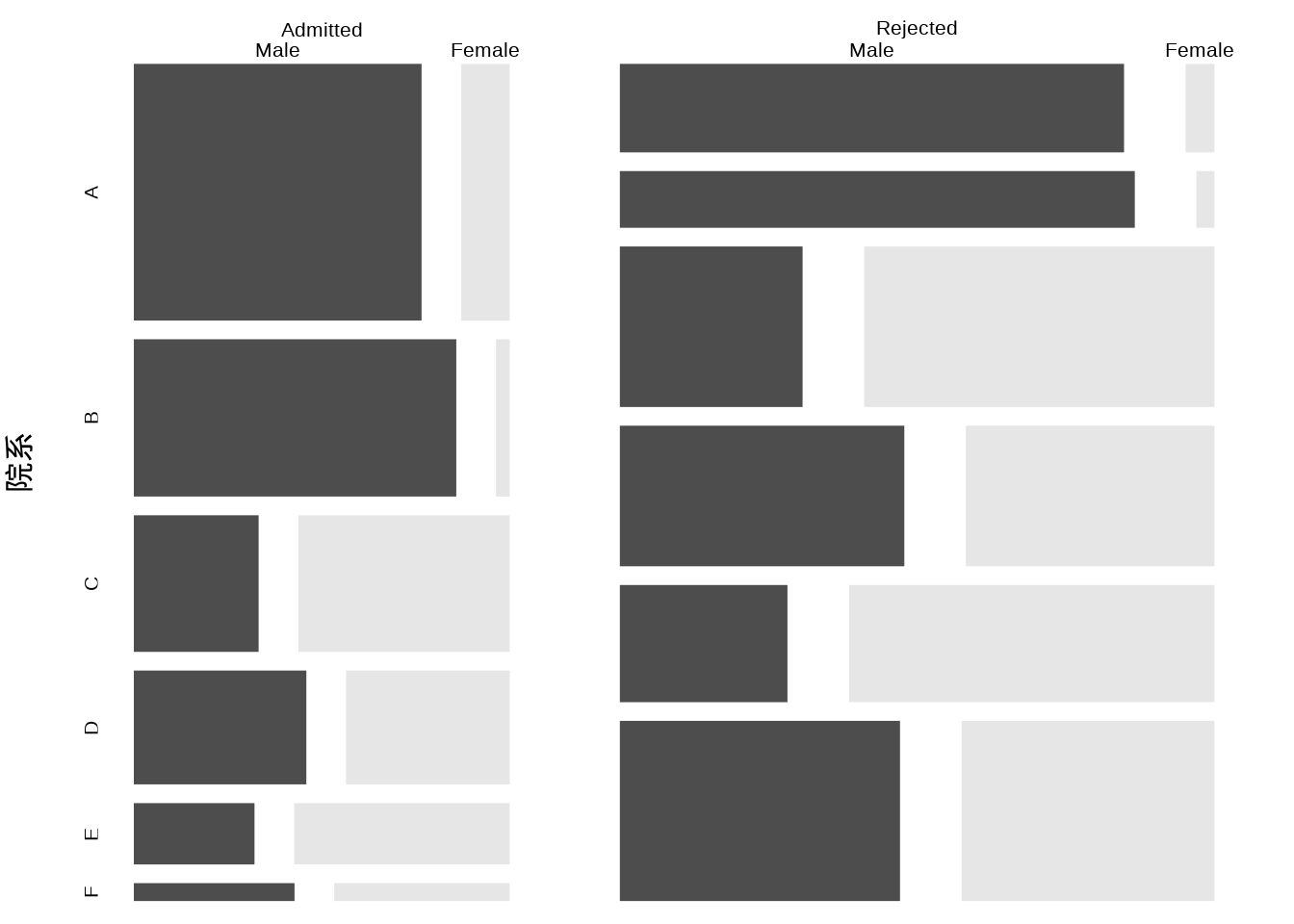
接下来进行定量的分析，首先，按性别和录取情况统计人数，如下：

m <- xtabs(Freq ~ Gender + Admit, data = as.data.frame(UCBAdmissions))
m

#>         Admit
#> Gender   Admitted Rejected
#>   Male       1198     1493
#>   Female      557     1278

可以看到，申请加州伯克利分校的女生当中，只有 \(557 / (557 + 1278) = 30.35\%\) 录取了，而男生则有 \(1198 / (1198 + 1493) = 44.52\%\) 的录取率。根据皮尔逊 \(\chi^2\) 检验：

# 不带耶茨矫正
chisq.test(m, correct = FALSE)

#> 
#>  Pearson's Chi-squared test
#> 
#> data:  m
#> X-squared = 92.205, df = 1, p-value < 2.2e-16

可知 \(\chi^2\) 统计量的值为 \(92.205\) 且 P 值远远小于 0.05， 差异达到统计显著性，不是随机因素导致的。因此，加州伯克利分校被指控在招生录取工作中存在性别歧视。然而，当我们细分到各个院系去看录取率（录取人数 / 申请人数），结果显示院系 A 的录取率为 64.41%，院系 B 的录取率为 63.24%，依次类推，各院系情况如下：

proportions(xtabs(Freq ~ Dept + Admit,
  data = as.data.frame(UCBAdmissions)
), margin = 1)

#>     Admit
#> Dept   Admitted   Rejected
#>    A 0.64415863 0.35584137
#>    B 0.63247863 0.36752137
#>    C 0.35076253 0.64923747
#>    D 0.33964646 0.66035354
#>    E 0.25171233 0.74828767
#>    F 0.06442577 0.93557423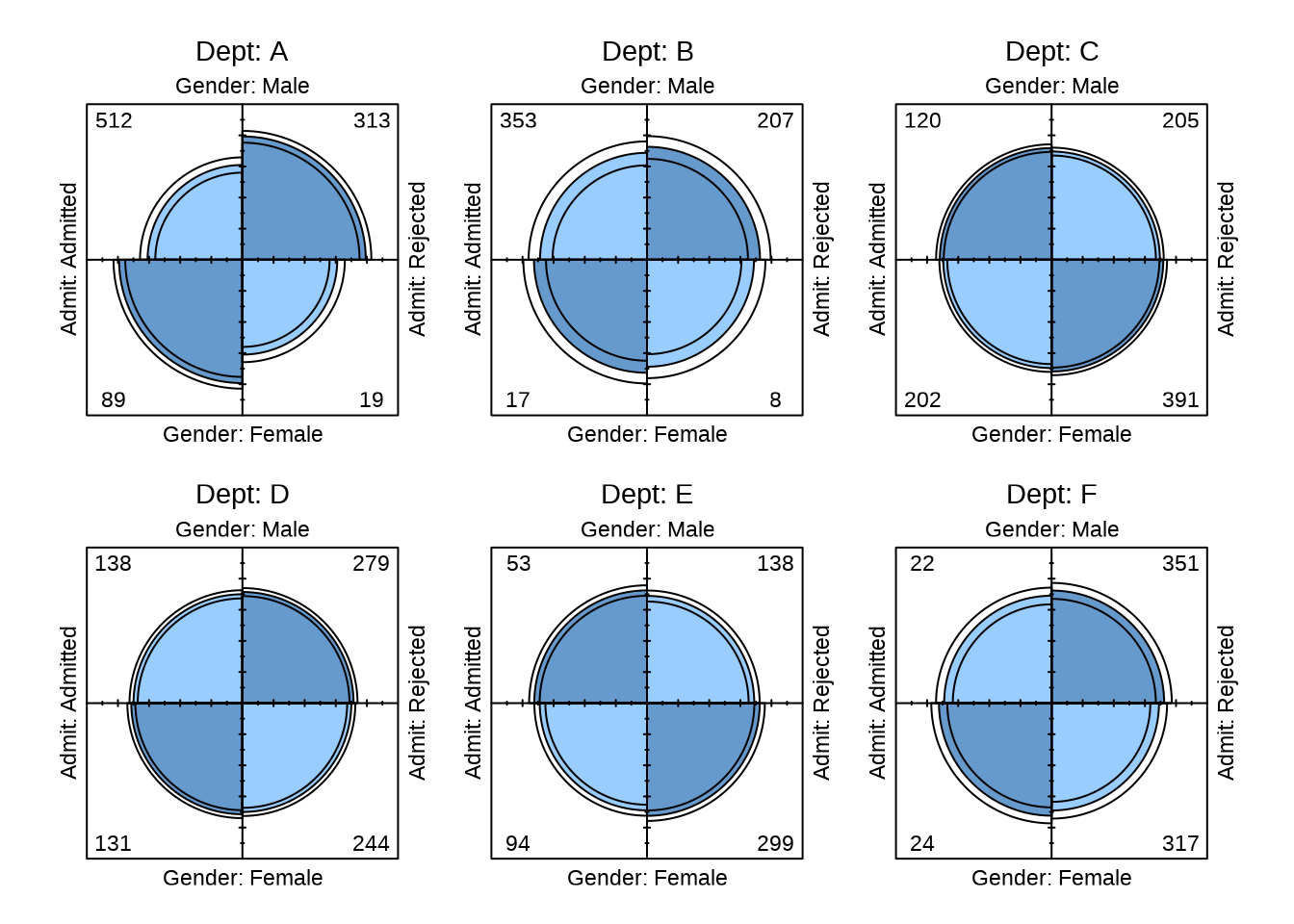

图 14.6: 加州伯克利分校各院系录取情况

对每个院系，单独使用皮尔逊 \(\chi^2\) 检验，发现只有 A 系的男、女生录取率的差异达到统计显著性，其它系的差异都不显著。辛普森悖论在这里出现了，在分类数据的分析中，常常遇到。

# 以 A 系为例
ma <- xtabs(Freq ~ Gender + Admit,
  subset = Dept == "A",
  data = as.data.frame(UCBAdmissions)
)
chisq.test(ma, correct = FALSE)

#> 
#>  Pearson's Chi-squared test
#> 
#> data:  ma
#> X-squared = 17.248, df = 1, p-value = 3.28e-05

为了经一步说明此现象的原因，建立对数线性模型来拟合数据，值得一提的是皮尔逊卡方检验可以从对数线性模型的角度来看，而对数线性模型是一种特殊的广义线性模型，针对计数数据建模。

fit_ucb0 <- glm(Freq ~ Dept + Admit + Gender,
  family = poisson(link = "log"),
  data = as.data.frame(UCBAdmissions)
)
summary(fit_ucb0)

#> 
#> Call:
#> glm(formula = Freq ~ Dept + Admit + Gender, family = poisson(link = "log"), 
#>     data = as.data.frame(UCBAdmissions))
#> 
#> Coefficients:
#>               Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)    5.37111    0.03964 135.498  < 2e-16 ***
#> DeptB         -0.46679    0.05274  -8.852  < 2e-16 ***
#> DeptC         -0.01621    0.04649  -0.349 0.727355    
#> DeptD         -0.16384    0.04832  -3.391 0.000696 ***
#> DeptE         -0.46850    0.05276  -8.879  < 2e-16 ***
#> DeptF         -0.26752    0.04972  -5.380 7.44e-08 ***
#> AdmitRejected  0.45674    0.03051  14.972  < 2e-16 ***
#> GenderFemale  -0.38287    0.03027 -12.647  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for poisson family taken to be 1)
#> 
#>     Null deviance: 2650.1  on 23  degrees of freedom
#> Residual deviance: 2097.7  on 16  degrees of freedom
#> AIC: 2272.7
#> 
#> Number of Fisher Scoring iterations: 5

添加性别和院系的交互效应后，对数线性模型的 AIC 下降一半多，说明模型的交互效应是显著的，也就是说性别和院系之间存在非常强的关联。

fit_ucb1 <- glm(Freq ~ Dept + Admit + Gender + Dept * Gender,
  family = poisson(link = "log"),
  data = as.data.frame(UCBAdmissions)
)
summary(fit_ucb1)

#> 
#> Call:
#> glm(formula = Freq ~ Dept + Admit + Gender + Dept * Gender, family = poisson(link = "log"), 
#>     data = as.data.frame(UCBAdmissions))
#> 
#> Coefficients:
#>                    Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)         5.76801    0.03951 145.992  < 2e-16 ***
#> DeptB              -0.38745    0.05475  -7.076 1.48e-12 ***
#> DeptC              -0.93156    0.06549 -14.224  < 2e-16 ***
#> DeptD              -0.68230    0.06008 -11.356  < 2e-16 ***
#> DeptE              -1.46311    0.08030 -18.221  < 2e-16 ***
#> DeptF              -0.79380    0.06239 -12.722  < 2e-16 ***
#> AdmitRejected       0.45674    0.03051  14.972  < 2e-16 ***
#> GenderFemale       -2.03325    0.10233 -19.870  < 2e-16 ***
#> DeptB:GenderFemale -1.07581    0.22860  -4.706 2.52e-06 ***
#> DeptC:GenderFemale  2.63462    0.12343  21.345  < 2e-16 ***
#> DeptD:GenderFemale  1.92709    0.12464  15.461  < 2e-16 ***
#> DeptE:GenderFemale  2.75479    0.13510  20.391  < 2e-16 ***
#> DeptF:GenderFemale  1.94356    0.12683  15.325  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for poisson family taken to be 1)
#> 
#>     Null deviance: 2650.10  on 23  degrees of freedom
#> Residual deviance:  877.06  on 11  degrees of freedom
#> AIC: 1062.1
#> 
#> Number of Fisher Scoring iterations: 5

此辛普森悖论现象的解释是女生倾向于申请录取率低的院系，而男生倾向于申请录取率高的院系，最终导致整体上，男生的录取率显著高于女生。至于为什么女生会倾向于申请录取率低的院系？这可能要看具体的院系是哪些，招生政策如何？这已经不是仅仅依靠招生办的统计数字就可以完全解释得了的，更多详情见文献 Bickel, Hammel, 和 O’Connell (1975) 。

提示

对数线性模型的皮尔逊 \(\chi^2\) 检验的统计量

sum(residuals(fit_ucb1, type = "pearson")^2)

#> [1] 797.7045

比较多个广义线性模型的拟合效果，除了看 AIC，还可以看对数似然，它越大越好。可以看到添加性别和院系的交互效应后，对数似然增加了一倍多。

# 基础模型
logLik(fit_ucb0)

#> 'log Lik.' -1128.365 (df=8)

# 添加交互效应
logLik(fit_ucb1)

#> 'log Lik.' -518.0581 (df=13)

14.6 分析泰坦尼克号乘客生存率

分析存活率的影响因素。

除了从条件独立性检验的角度，下面从逻辑回归模型的角度分析这个高维列联表数据，由此，我们可以知道假设检验和广义线性模型之间的联系，针对复杂高维列联表数据进行关联分析和解释。

响应变量是乘客的状态，存活还是死亡，titanic_data 是按船舱 Class、性别 Sex 和年龄 Age 分类汇总统计的数据，因此，下面的逻辑回归模型是对乘客群体的建模。

# 建立模型
fit_titanic <- glm(cbind(Freq_Yes, Freq_No) ~ Class + Sex + Age,
  data = titanic_data, family = binomial(link = "logit")
)

接着，我们查看模型输出的情况

# 模型输出
summary(fit_titanic)

#> 
#> Call:
#> glm(formula = cbind(Freq_Yes, Freq_No) ~ Class + Sex + Age, family = binomial(link = "logit"), 
#>     data = titanic_data)
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)   0.6853     0.2730   2.510   0.0121 *  
#> Class2nd     -1.0181     0.1960  -5.194 2.05e-07 ***
#> Class3rd     -1.7778     0.1716 -10.362  < 2e-16 ***
#> ClassCrew    -0.8577     0.1573  -5.451 5.00e-08 ***
#> SexFemale     2.4201     0.1404  17.236  < 2e-16 ***
#> AgeAdult     -1.0615     0.2440  -4.350 1.36e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 671.96  on 13  degrees of freedom
#> Residual deviance: 112.57  on  8  degrees of freedom
#> AIC: 171.19
#> 
#> Number of Fisher Scoring iterations: 5

Agresti, Alan. 2007. An Introduction to Categorical Data Analysis. 2nd 本. Hoboken, New Jersey: John Wiley & Sons, Inc.

Bickel, P. J., E. A. Hammel, 和 J. W. O’Connell. 1975. 《Sex Bias in Graduate Admissions: Data from Berkeley》. Science 187 (4175): 398–404. https://doi.org/10.1126/science.187.4175.398.

Brunson, Jason Cory. 2020. 《ggalluvial: Layered Grammar for Alluvial Plots》. Journal of Open Source Software 5 (49): 2017. https://doi.org/10.21105/joss.02017.

Clopper, C. J., 和 E. S. Pearson. 1934. 《The Use of Confidence or Fiducial Limits Illustrated In The Case of The Binomial》. Biometrika 26 (4): 404–13. https://doi.org/10.1093/biomet/26.4.404.

Friendly, Michael, 和 David Meyer. 2016. Discrete Data Analysis with R: Visualization and Modeling Techniques for Categorical and Count Data. 1st 本. Boca Raton, Florida: Chapman; Hall/CRC.

Meyer, David, Achim Zeileis, 和 Kurt Hornik. 2006. 《The Strucplot Framework: Visualizing Multi-Way Contingency Tables with vcd》. Journal of Statistical Software 17 (3): 1–48. https://doi.org/10.18637/jss.v017.i03.

Newcombe, Robert G. 1998. 《Interval estimation for the difference between independent proportions: comparison of eleven methods》. Statistics in Medicine 17 (8): 873–90. https://doi.org/10.1002/(SICI)1097-0258(19980430)17:8<873::AID-SIM779>3.0.CO;2-I.

Wilson, Edwin B. 1927. 《Probable inference, the law of succession, and statistical inference》. Journal of the American Statistical Association 22 (158): 209–12. https://doi.org/10.1080/01621459.1927.10502953.

Zeileis, Achim, David Meyer, 和 Kurt Hornik. 2007. 《Residual-based Shadings for Visualizing (Conditional) Independence》. Journal of Computational and Graphical Statistics 16 (3): 507–25. https://doi.org/10.1198/106186007X237856.

宋泽熙. 2011. 《两个二项总体成功概率的比较》. 中国校外教育（理论） z1: 81. https://doi.org/10.3969/j.issn.1004-8502-B.2011.z1.0919.

---

1. https://en.wikipedia.org/wiki/Ronald_Fisher