15.1 常微分方程

洛伦兹系统是一个常微分方程组，系统参数的默认值为 \((\sigma = 10, \rho = 28, \beta = 8/3)\)，初值为 \((-13, -14, 47)\)。

\[\begin{equation*} \left\{ \begin{array}{l} \frac{\partial x}{\partial t} = \sigma (y - x) \\ \frac{\partial y}{\partial t} = x(\rho -z) - y \\ \frac{\partial x}{\partial t} = xy - \beta z \end{array} \right. \end{equation*}\]

library(deSolve)
# 参数
pars <- c(a = -8 / 3, b = -10, c = 28)
# 初值
state <- c(X = 1, Y = 1, Z = 1)
# 时间间隔
times <- seq(0, 100, by = 0.01)
# 定义方程组
lorenz_fun <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
    dX <- a * X + Y * Z
    dY <- b * (Y - Z)
    dZ <- -X * Y + c * Y - Z
    list(c(dX, dY, dZ))
  })
}
out <- ode(
  y = state, times = times,
  func = lorenz_fun, parms = pars
)

调用 scatterplot3d 绘制三维曲线图，如图15.1 所示

library(scatterplot3d)

scatterplot3d(
  x = out[, "X"], y = out[, "Y"], z = out[, "Z"],
  col.axis = "black", type = "l", color = "gray",
  xlab = expression(x), ylab = expression(y), zlab = expression(z),
  col.grid = "gray", main = "Lorenz"
)

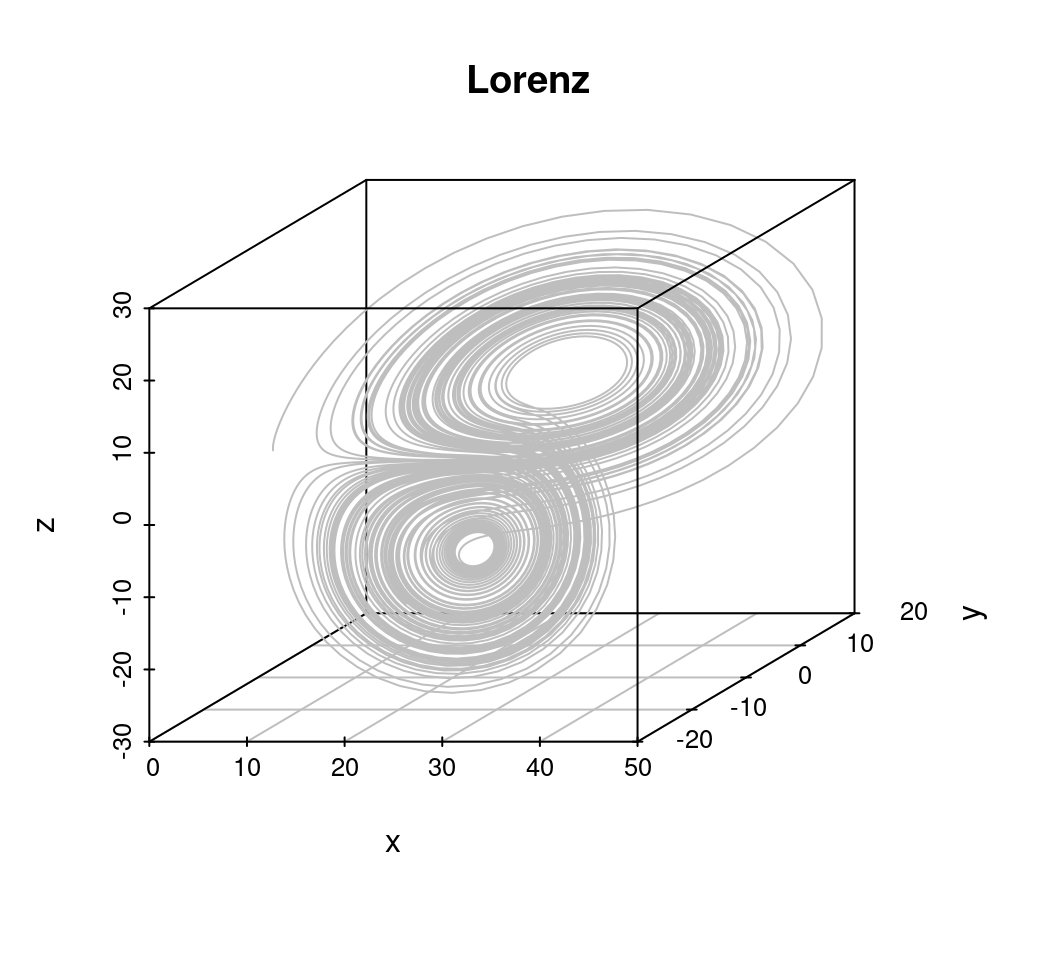
图 15.1: 洛伦兹曲线