14.3 二次规划
14.3.1 凸二次规划
在 R 中使用 quadprog [33] 包求解二次规划45,quadprogXT 包用来求解带绝对值约束的二次规划,pracma [34]包提供 quadprog() 函数就是对 quadprog 包的 solve.QP() 进行封装,调用风格更像 Matlab。quadprog 包实现了 Goldfarb and Idnani (1982, 1983) 提出的对偶方法,主要用来求解带线性约束的严格凸二次规划问题。quadprog 求解的二次型的形式如下:
\[\min_b - d^{\top}b +\frac{1}{2}b^{\top}Db , \quad A^{\top}b \geq b_{0}\]
solve.QP(Dmat, dvec, Amat, bvec, meq = 0, factorized = FALSE)参数 Dmat、dvec、Amat、bvec 分别对应二次规划问题中的 \(D,d,A,b_{0}\)。下面举个二次规划的具体例子
\[ D = \begin{bmatrix}2 & -1\\ -1 & 2 \end{bmatrix}, \quad d = (-3,2), \quad A = \begin{bmatrix}1 & 1\\ -1 & 1 \\ 0 & -1 \end{bmatrix}, \quad b_{0} = (2,-2,-3) \]
即目标函数 \[Q(x,y) = x^2 + y^2 -xy+3x-2y+4\] 它的可行域如图14.1所示
plot(0, 0,
xlim = c(-2, 5.5), ylim = c(-1, 3.5), type = "n",
xlab = "x", ylab = "y", main = "Feasible Region"
)
polygon(c(2, 5, -1), c(0, 3, 3), border = TRUE, lwd = 2, col = "gray")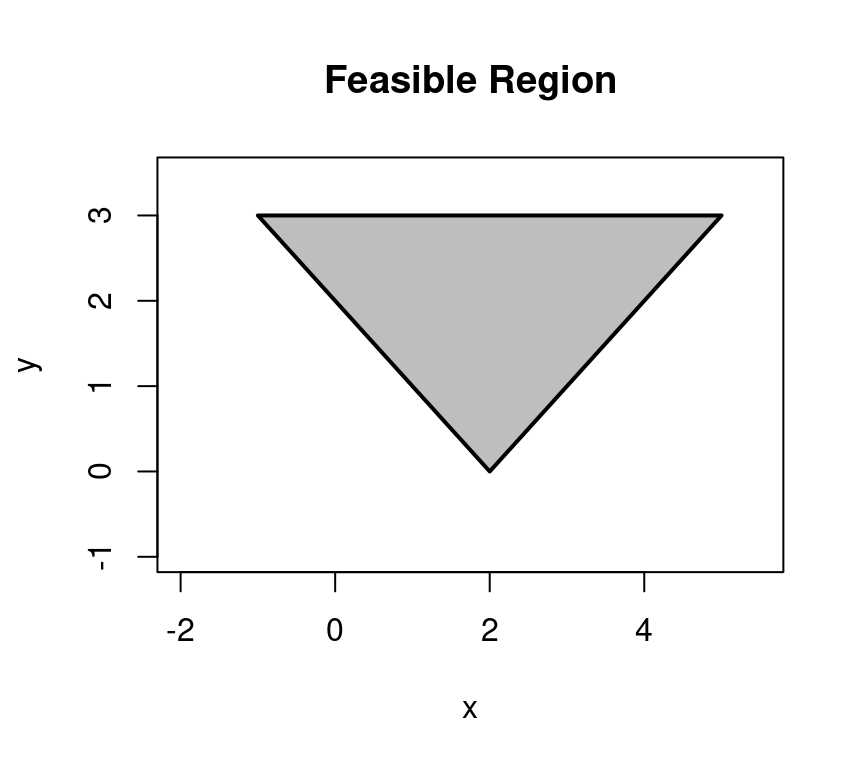
图 14.1: 可行域
调用 quadprog 包的 solve.QP() 函数求解此二次规划问题
library(quadprog)
Dmat <- matrix(c(2, -1, -1, 2), nrow = 2, byrow = TRUE)
dvec <- c(-3, 2)
A <- matrix(c(1, 1, -1, 1, 0, -1), ncol = 2, byrow = TRUE)
bvec <- c(2, -2, -3)
Amat <- t(A)
sol <- solve.QP(Dmat = Dmat, dvec = dvec, Amat = Amat, bvec = bvec)
sol## $solution
## [1] 0.1666667 1.8333333
##
## $value
## [1] -0.08333333
##
## $unconstrained.solution
## [1] -1.3333333 0.3333333
##
## $iterations
## [1] 2 0
##
## $Lagrangian
## [1] 1.5 0.0 0.0
##
## $iact
## [1] 1ROI 默认的二次规划的标准形式为 \(\frac{1}{2}x^{\top}Qx + a^{\top}x\),在传递参数值的时候注意和上面的区别。
library(ROI)
op <- OP(
objective = Q_objective(Q = Dmat, L = -dvec),
constraints = L_constraint(A, rep(">=", 3), bvec),
maximum = FALSE # 默认求最小
)
nlp <- ROI_solve(op, solver = "nloptr.slsqp", start = c(1, 2))
nlp$objval## [1] -0.08333333nlp$solution## [1] 0.1666667 1.833333314.3.2 半正定二次优化
kernlab 提供基于核的机器学习方法,可用于分类、回归、聚类、异常检测、分位回归、降维等场景,包含支撑向量机、谱聚类、核PCA、高斯过程和二次规划求解器,将优化方法用于机器学习,展示二者的关系。
R 包 kernlab 的函数 ipop() 实现内点法可以求解半正定的二次规划问题,对应到上面的例子,就是要求 \(A \geq 0\),而 R 包 quadprog 只能求解正定的二次规划问题,即要求 \(A > 0\)。
以二分类问题为例,采用 SMO (Sequential Minimization Optimization) 求解器,将 SVM 的二次优化问题分解。
library(kernlab)
set.seed(123)
x <- rbind(matrix(rnorm(120), 60, 2), matrix(rnorm(120, mean = 3), 60, 2))
y <- matrix(c(rep(1, 60), rep(-1, 60)))
svp <- ksvm(x, y, type = "C-svc")
plot(svp, data = x)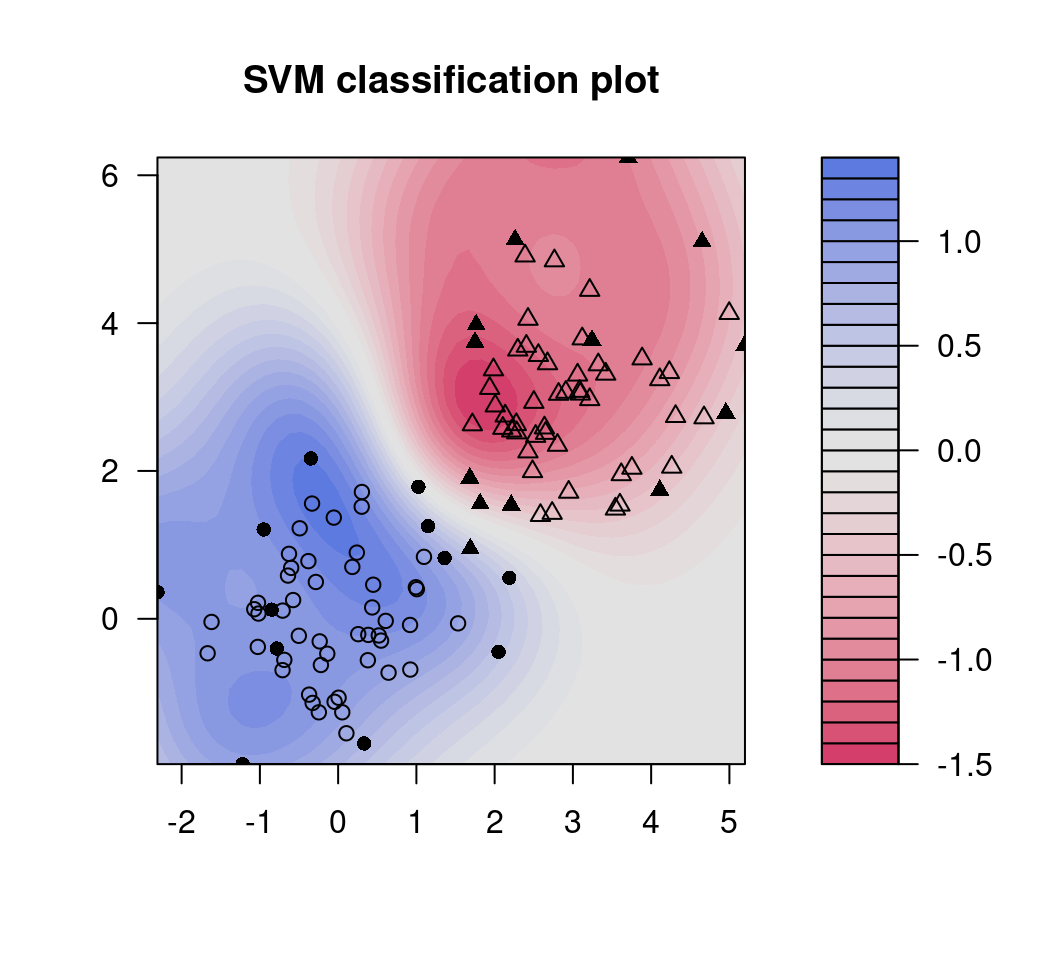
图 14.2: 二分类问题